List of mathematical symbols by subject
This list of mathematical symbols by subject shows a selection of the most common symbols that are used in modern mathematical notation within formulas, grouped by mathematical topic. As it is virtually impossible to list all the symbols ever used in mathematics, only those symbols which occur often in mathematics or mathematics education are included. Many of the characters are standardized, for example in DIN 1302 General mathematical symbols or DIN EN ISO 80000-2 Quantities and units – Part 2: Mathematical signs for science and technology.
The following list is largely limited to non-alphanumeric characters. It is divided by areas of mathematics and grouped within sub-regions. Some symbols have a different meaning depending on the context and appear accordingly several times in the list. Further information on the symbols and their meaning can be found in the respective linked articles.
Guide
The following information is provided for each mathematical symbol:
- Symbol
- The symbol as it is represented by LaTeX. If there are several typographic variants, only one of the variants is shown.
- Usage
- An exemplary use of the symbol in a formula. Letters here stand as a placeholder for numbers, variables or complex expressions. Different possible applications are listed separately.
- Interpretation
- A short textual description of the meaning of the formula in the previous column.
- Article
- The Wikipedia article that discusses the meaning (semantics) of the symbol.
- LaTeX
- The LaTeX command that creates the icon. Characters from the ASCII character set can be used directly, with a few exceptions (pound sign #, backslash \, braces {}, and percent sign %). High-and low-position is indicated via the characters ^ and _ and is not explicitly specified.
- HTML
- The icon in HTML, if it is defined as a named mark. Non-named characters can be indicated in the form can &#xnnnn by specifying the Unicode code point of the next column. High-and low-position can be indicated via <sup></sup> and <sub></sub>.
- Unicode
- The code point of the corresponding Unicode character. Some characters are combining and require the entry of additional characters. For brackets, the code points of the opening and the closing forms are specified.
Set theory
Definition symbols
| Symbol |
Usage |
Interpretation |
Article |
LaTeX |
HTML |
Unicode |
|---|
 |
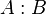 |
 is defined by is defined by  |
Definition |
: |
|
U+003A |
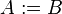 |
 is defined as equal to is defined as equal to  |
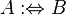 |
 is defined as equivalent to is defined as equivalent to  |
Set construction
| Symbol |
Usage |
Interpretation |
Article |
LaTeX |
HTML |
Unicode |
|---|
 |
|
Empty set |
Empty set |
\varnothing,
\emptyset |
∅ |
U+2205 |
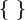 |
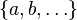 |
Set consisting of the elements  and so on and so on |
Set (mathematics) |
\{ \} |
|
U+007B/D |
 |
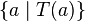 |
Set of elements  , that satisfy the condition , that satisfy the condition 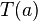 |
\mid |
|
U+007C |
 |
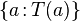 |
\colon |
|
U+003A |
Set operations
Set relations
| Symbol |
Usage |
Interpretation |
Article |
LaTeX |
HTML |
Unicode |
|---|
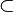 |
 |
 is a proper subset of is a proper subset of  |
Subset |
\subset |
⊂ |
U+2282 |
 |
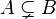 |
\subsetneq |
|
U+228A |
 |
 |
 is a subset of is a subset of  |
\subseteq |
⊆ |
U+2286 |
 |
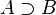 |
 is a proper superset of is a proper superset of  |
Superset |
\supset |
⊃ |
U+2283 |
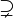 |
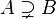 |
\supsetneq |
|
U+228B |
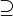 |
 |
 is a superset of is a superset of  |
\supseteq |
⊇ |
U+2287 |
 |
 |
Element  is in the set is in the set  |
Element (mathematics) |
\in |
∈ |
U+2208 |
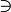 |
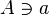 |
\ni, \owns |
∋ |
U+220B |
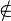 |
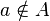 |
Element  is not in the set is not in the set  |
\notin |
∉ |
U+2209 |
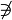 |
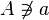 |
\not\ni |
|
U+220C |
Note: The symbols 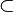 and
and  are used inconsistently and often do not exclude the equality of the two quantities.
are used inconsistently and often do not exclude the equality of the two quantities.
Number sets
Cardinality
Arithmetic
Arithmetic operators
| Symbol |
Usage |
Interpretation |
Article |
LaTeX |
HTML |
Unicode |
|---|
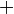 |
 |
 added to added to  |
Addition |
+ |
|
U+002B |
 |
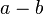 |
 subtracted from subtracted from  |
Subtraction |
- |
|
U+2212 |
 |
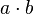 |
 multiplied by multiplied by  |
Multiplication |
\cdot |
· |
U+22C5 |
 |
 |
\times |
× |
U+2A2F |
 |
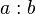 |
 divided by divided by  |
Division (mathematics) |
: |
|
U+003A |
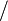 |
 |
/ |
⁄ |
U+2215 |
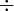 |
 |
\div |
÷ |
U+00F7 |
 |
 |
\frac |
|
U+2044 |
 |
 |
Negative of the number  or the additive inverse of or the additive inverse of  |
Unary minus |
- |
− |
U+2212 |
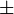 |
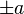 |
Plus or minus  |
Plus or minus sign |
\pm |
± |
U+00B1 |
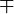 |
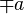 |
Minus or plus  |
\mp |
|
U+2213 |
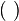 |
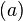 |
Term  is evaluated first is evaluated first |
Bracket |
( ) |
|
U+0028/9 |
![[~]](../I/m/8fd6f25a2c5baf0b452ad209974c725c.png) |
![[a]](../I/m/88164354652817ffee36d596a683a2d4.png) |
[ ] |
|
U+005B/D |
Equality signs
Comparison
| Symbol |
Usage |
Interpretation |
Article |
LaTeX |
HTML |
Unicode |
|---|
 |
 |
 is less than is less than  |
Comparison (mathematics) |
< |
< |
U+003C |
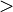 |
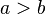 |
 is greater than is greater than  |
> |
> |
U+003E |
 |
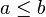 |
 is less than or equal to is less than or equal to  |
\le, \leq |
≤ |
U+2264 |
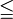 |
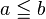 |
\leqq |
|
U+2266 |
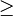 |
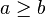 |
 is greater than or equal to is greater than or equal to  |
\ge, \geq |
≥ |
U+2265 |
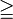 |
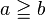 |
\geqq |
|
U+2267 |
 |
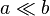 |
 is much smaller than is much smaller than  |
\ll |
|
U+226A |
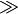 |
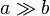 |
 is much bigger than is much bigger than  |
\gg |
|
U+226B |
Divisibility
Intervals
| Symbol |
Usage |
Interpretation |
Article |
LaTeX |
HTML |
Unicode |
|---|
![[~~]](../I/m/cac765c5f200573ea4d7eba350e4c607.png) |
![[a,b]](../I/m/2c3d331bc98b44e71cb2aae9edadca7e.png) |
Closed interval between  and and  |
Interval (mathematics) |
( )
[ ] |
|
U+0028/9
U+005B/D |
![]~~[](../I/m/7d22940947547c5e4be72378b1bd38e5.png) |
![]a,b[](../I/m/e46b2a760c57eb995b62bd166b835b1e.png) |
Open interval between  and and  |
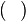 |
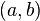 |
 |
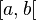 |
Right-open interval between  and and  |
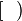 |
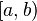 |
![]~~]](../I/m/d3847530971a7bed5d94340aceccc821.png) |
![]a,b]](../I/m/eeac36b17358aa3ca5516b59003d1560.png) |
Left-open interval between  and and  |
![(~~]](../I/m/d05afd0f1d6d3c620335ad29ff676fd3.png) |
![(a,b]](../I/m/a33b8ca44ded30abf82b7dca332e9a96.png) |
Elementary functions
| Symbol |
Usage |
Interpretation |
Article |
LaTeX |
HTML |
Unicode |
|---|
 |
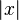 |
Absolute value of  |
Absolute value |
\vert |
|
U+007C |
![\left[ ~~ \right]](../I/m/e10fc02cad552ee3fcfaee4e52ab6bec.png) |
![\left[ x \right]](../I/m/4fcbf9b418b2ad4ef36169fb15a32bdd.png) |
Biggest whole number less than or equal to  |
Floor and ceiling functions |
[ ] |
|
U+005B/D |
 |
 |
\lfloor \rfloor |
⌊ ⌋ |
U+230A/B |
 |
 |
Smallest whole number greater than or equal to  |
\lceil \rceil |
⌈ ⌉ |
U+2308/9 |
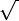 |
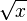 |
Square root of  |
Square root |
\sqrt |
√ |
U+221A |
![\sqrt[n]{x}](../I/m/5e4352778f3b156f05ef056f9793ec36.png) |
 -th root of -th root of  |
nth root |
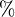 |
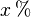 |
 percent percent |
Percent |
\% |
|
U+0025 |
Note: the power function is not represented by its own icon, but by the positioning of the exponent as a superscript.
Complex numbers
| Symbol |
Usage |
Interpretation |
Article |
LaTeX |
HTML |
Unicode |
|---|
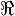 |
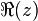 |
Real part of complex number 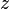 |
Complex number |
\Re |
|
U+211C |
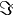 |
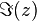 |
Imaginary part of complex number 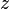 |
\Im |
|
U+2111 |
 |
 |
Complex conjugate of 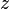 |
Complex conjugate |
\bar |
|
U+0305 |
 |
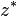 |
\ast |
∗ |
U+002A |
 |
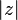 |
Absolute value of complex number 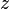 |
Absolute value |
\vert |
|
U+007C |
- Remark: real and complex parts of a complex number are often also denoted by
 and
and 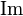 .
.
Mathematical constants
| Symbol |
Usage |
Interpretation |
Article |
LaTeX |
HTML |
Unicode |
|---|
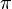 |
|
Pi, or Archimedes' constant |
Pi |
\pi |
π |
U+03C0 |
 |
|
Euler's constant |
e (mathematics) |
\rm{e} |
|
U+0065 |
 |
|
Golden ratio |
Golden ratio |
\varphi |
φ |
U+03C6 |
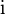 |
|
Imaginary unit (square root of −1) |
Imaginary unit |
\rm{i} |
|
U+0069 |
See also: mathematical constant for symbols of additional mathematical constants.
Calculus
Sequences and series
| Symbol |
Usage |
Interpretation |
Article |
LaTeX |
HTML |
Unicode |
|---|
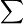 |
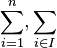 |
Sum from  to to  or over all elements or over all elements  in set in set  |
Summation |
\sum |
∑ |
U+2211 |
 |
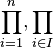 |
Product from  to to  or over all elements or over all elements  in set in set  |
Product (mathematics) |
\prod |
∏ |
U+220F |
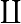 |
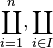 |
Coproduct from  to to  or over all elements or over all elements  in set in set  |
Coproduct |
\coprod |
|
U+2210 |
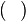 |
 |
Sequence of elements 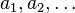 |
Sequence |
( ) |
|
U+0028/9 |
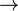 |
 |
Sequence  tends to limit tends to limit  |
Limit of a sequence |
\to |
→ |
U+2192 |
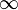 |
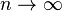 |
 tends to infinity tends to infinity |
Infinity |
\infty |
∞ |
U+221E |
Functions
Limits
| Symbol |
Usage |
Interpretation |
Article |
LaTeX |
HTML |
Unicode |
|---|
 |
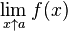 |
Limit of function  as as  approaches approaches  from below from below |
Limit of a function |
\uparrow |
↑ |
U+2191 |
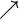 |
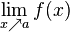 |
\nearrow |
|
U+2197 |
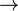 |
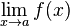 |
Limit of function  as as  approaches approaches  |
\to |
→ |
U+2192 |
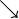 |
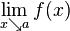 |
Limit of function  as as  approaches approaches  from above from above |
\searrow |
|
U+2198 |
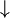 |
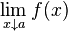 |
\downarrow |
↓ |
U+2193 |
Asymptotic behaviour
| Symbol |
Usage |
Interpretation |
Article |
LaTeX |
HTML |
Unicode |
|---|
 |
 |
Function  is asymptotically equal to function is asymptotically equal to function  |
Asymptotic analysis |
\sim |
∼ |
U+223C |
 |
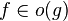 |
Function  grows slower than grows slower than  |
Big O notation |
o |
|
U+006F |
 |
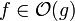 |
Function  grows not substantially faster than grows not substantially faster than  |
\mathcal{O} |
|
U+1D4AA |
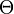 |
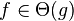 |
Function  grows as fast as grows as fast as  |
\Theta |
Θ |
U+0398 |
 |
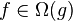 |
Function  grows not substantially slower than grows not substantially slower than  |
\Omega |
Ω |
U+03A9 |
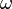 |
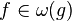 |
Function  grows faster than grows faster than  |
\omega |
ω |
U+03C9 |
Differential calculus
| Symbol |
Usage |
Interpretation |
Article |
LaTeX |
HTML |
Unicode |
|---|
 |
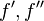 |
First or second derivative of function  |
Differentiation (mathematics) |
\prime |
′ |
U+2032 |
 |
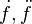 |
First or second derivative of function  with respect to time (in physics) with respect to time (in physics) |
\dot, \ddot |
|
U+0307 |
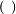 |
 |
 -th derivative of function -th derivative of function  |
( ) |
|
U+0028/9 |
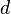 |
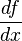 |
Derivative of function  with respect to variable with respect to variable  |
d |
|
U+0064 |
 |
Total differential of function  |
Total differential |
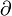 |
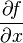 |
Partial derivative of function  with respect to variable with respect to variable  |
Partial derivative |
\partial |
∂ |
U+2202 |
Integral calculus
| Symbol |
Usage |
Interpretation |
Article |
LaTeX |
HTML |
Unicode |
|---|
 |
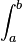 , , 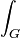 |
Definite integral between  and and  or over set or over set  |
Integral |
\int |
∫ |
U+222B |
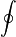 |
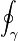 |
Curve integral along curve 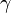 |
Curve integral |
\oint |
|
U+222E |
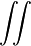 |
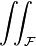 |
Surface integral over surface 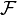 |
Surface integral |
\iint |
|
U+222C |
 |
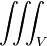 |
Volume integral over volume  |
Volume integral |
\iiint |
|
U+222D |
Vector calculus
Topology
Functional analysis
| Symbol |
Usage |
Interpretation |
Article |
LaTeX |
HTML |
Unicode |
|---|
 |
 |
Topological dual space of topological vector space  |
Dual space |
\prime |
′ |
U+2032 |
 |
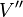 |
Bidual space of normed vector space  |
 |
 |
Completion of metric space  |
Complete metric space |
\hat |
|
U+0302 |
 |
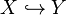 |
Embedding of topological vector space  into into 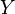 |
Embedding |
\hookrightarrow |
|
U+21AA |
Linear algebra and geometry
Elementary geometry
| Symbol |
Usage |
Interpretation |
Article |
LaTeX |
HTML |
Unicode |
|---|
![[~~]](../I/m/cac765c5f200573ea4d7eba350e4c607.png) |
![[AB]](../I/m/5e32d4dbe98ef3af1b5123ccba43cbf7.png) |
Line segment between points  and and  |
Line segment |
[ ] |
|
U+005B/D |
 |
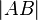 |
Length of line segment between points  and and  |
\vert |
|
U+007C |
 |
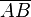 |
\overline |
|
U+0305 |
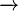 |
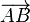 |
Vector between points  and and  |
Euclidean vector |
\vec |
|
U+20D7 |
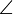 |
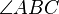 |
Angle between line segments 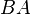 and and 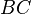 |
Angle |
\angle |
∠ |
U+2220 |
 |
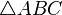 |
Triangle with vertices  , ,  and and 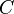 |
Triangle |
\triangle |
|
U+25B3 |
 |
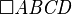 |
Quadrilateral with vertices  , ,  , , 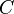 and and  |
Quadrilateral |
\square |
|
U+25A1 |
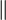 |
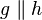 |
Lines  and and  are parallel are parallel |
Parallel (geometry) |
\parallel |
|
U+2225 |
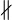 |
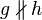 |
Lines  and and  are not parallel are not parallel |
\nparallel |
|
U+2226 |
 |
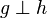 |
Lines  and and  are orthogonal are orthogonal |
Orthogonality |
\perp |
⊥ |
U+27C2 |
Vectors and matrices
| Symbol |
Interpretation |
Article |
LaTeX |
|---|
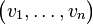 |
Row vector comprising elements  through through  |
Vector (mathematics and physics) |
\begin{pmatrix}
...
\end{pmatrix}
oder
\left(
\begin{array}{...}
...
\end{array}
\right) |
 |
Column vector comprising elements  through through 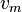 |
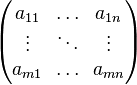 |
Matrix comprising elements  through through 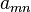 |
Matrix (mathematics) |
Vector calculus
| Symbol |
Usage |
Interpretation |
Article |
LaTeX |
HTML |
Unicode |
|---|
 |
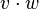 |
Dot product of vectors 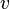 and and  |
Dot product |
\cdot |
· |
U+22C5 |
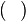 |
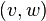 |
( ) |
|
U+0028/9 |
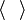 |
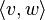
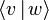 |
\langle \rangle |
⟨ ⟩ |
U+27E8/9 |
 |
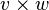 |
Cross product of vectors 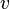 and and  |
Cross product |
\times |
× |
U+2A2F |
![[~~]](../I/m/cac765c5f200573ea4d7eba350e4c607.png) |
![[v,w]](../I/m/8820ef1eb7856a10b6bf90f90360cb0d.png) |
[ ] |
|
U+005B/D |
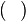 |
 |
Triple product of vectors 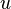 , , 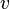 and and  |
Triple product |
( ) |
|
U+0028/9 |
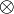 |
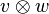 |
Dyadic product of vectors 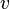 and and  |
Dyadic product |
\otimes |
⊗ |
U+2297 |
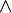 |
 |
Wedge product of vectors 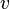 and and  |
Wedge product |
\wedge |
|
U+2227 |
 |
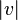 |
Length of vector 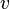 |
Euclidean norm |
\vert |
|
U+007C |
 |
 |
Norm of vector 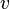 |
Norm (mathematics) |
\Vert, \| |
|
U+2016 |
 |
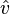 |
Normalized vector of vector 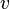 |
Unit vector |
\hat |
|
U+0302 |
Matrix calculus
Vector spaces
| Symbol |
Usage |
Interpretation |
Article |
LaTeX |
HTML |
Unicode |
|---|
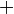 |
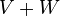 |
Sum of vector spaces  and and 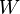 |
Direct sum of modules |
+ |
|
U+002B |
 |
 |
Direct sum of vector spaces  and and 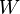 |
\oplus |
⊕ |
U+2295 |
 |
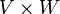 |
Direct product of vector spaces  and and 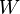 |
Direct product |
\times |
× |
U+2A2F |
 |
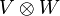 |
Tensor product of vector spaces  and and 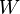 |
Tensor product |
\otimes |
⊗ |
U+2297 |
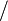 |
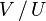 |
Quotient space of vector space  by subspace by subspace 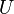 |
Quotient space (linear algebra) |
/ |
⁄ |
U+002F |
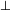 |
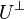 |
Orthogonal complement of subspace 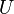 |
Orthogonal complement |
\perp |
⊥ |
U+27C2 |
 |
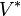 |
Dual space of vector space  |
Dual space |
\ast |
∗ |
U+002A |
 |
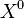 |
Annihilator space of the set of vectors  |
0 |
|
U+0030 |
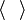 |
 |
Linear hull of the set of vectors  |
Linear hull |
\langle \rangle |
⟨ ⟩ |
U+27E8/9 |
Algebra
Relations
Group theory
Field theory
Ring theory
| Symbol |
Usage |
Interpretation |
Article |
LaTeX |
HTML |
Unicode |
|---|
 |
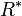 |
Group of units of ring  |
Group of units |
\ast |
∗ |
U+2217 |
 |
 |
\times |
× |
U+2A2F |
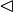 |
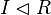 |
 is an ideal of ring is an ideal of ring  |
Ideal (ring theory) |
\vartriangleleft |
|
U+22B2 |
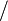 |
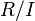 |
Quotient ring of ring  by ideal by ideal  |
Quotient ring |
/ |
⁄ |
U+002F |
![[ ~~ ]](../I/m/cac765c5f200573ea4d7eba350e4c607.png) |
![R[ X ]](../I/m/bc7fa5ab3a6d56e03880fba0532b0eca.png) |
Polynomial ring over ring  with variable with variable  |
Polynomial ring |
[ ] |
|
U+005B/D |
Combinatorics
| Symbol |
Usage |
Interpretation |
Article |
LaTeX |
HTML |
Unicode |
|---|
 |
 |
Number of permutations of  elements elements |
Factorial |
! |
|
U+0021 |
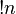 |
Number of derangements of  elements (permutations without fixed points) elements (permutations without fixed points) |
Derangement |
 |
Number of involutions without fixed points ( odd) odd) |
Double factorial |
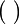 |
 |
Number of  -combinations of -combinations of  elements without repetition elements without repetition |
Combination |
\binom |
|
U+0028/9 |
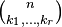 |
Number of permutations of  elements of which elements of which 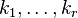 are identical are identical |
Multinomial coefficient |
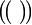 |
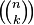 |
Number of  -combinations of -combinations of  elements with repetition elements with repetition |
Multiset |
|
|
U+0028/9 |
 |
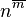 |
Rising factorial from  with with  factors factors |
Pochhammer symbol |
\overline |
|
U+0305 |
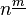 |
Falling factorial from  with with  factors factors |
\underline |
|
U+0332 |
 |
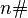 |
Product of all primes up to  |
Primorial |
\# |
|
U+0023 |
Stochastics
Probability theory
- Remark: for operators there are several notational variants; instead of round brackets also square brackets are used
Statistics
| Symbol |
Usage |
Interpretation |
Article |
LaTeX |
HTML |
Unicode |
|---|
 |
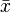 |
Average of the values  |
Average |
\bar |
|
U+0305 |
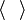 |
 |
Average over all values in the set  (in physics) (in physics) |
\langle \rangle |
⟨ ⟩ |
U+27E8/9 |
 |
 |
Estimator for parameter  |
Estimator |
\hat |
|
U+0302 |
Logic
Operators
| Symbol |
Usage |
Interpretation |
Article |
LaTeX |
HTML |
Unicode |
|---|
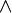 |
 |
Proposition  and proposition and proposition  |
Logical conjunction |
\land |
∧ |
U+2227 |
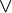 |
 |
Proposition  or proposition or proposition  (or both) (or both) |
Logical disjunction |
\lor |
∨ |
U+2228 |
 |
 |
Proposition  follows from proposition follows from proposition  and vice versa and vice versa |
Logical equivalence |
\Leftrightarrow |
⇔ |
U+21D4 |
 |
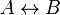 |
\leftrightarrow |
↔ |
U+2194 |
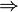 |
 |
From proposition  follows proposition follows proposition  |
Logical consequence |
\Rightarrow |
⇒ |
U+21D2 |
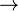 |
 |
\rightarrow |
→ |
U+2192 |
 |
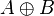 |
Either proposition  or proposition or proposition  |
Exclusive or |
\oplus |
⊕ |
U+2295 |
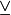 |
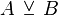 |
\veebar |
|
U+22BB |
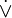 |
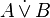 |
\dot\lor |
|
U+2A52 |
 |
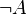 |
Not proposition  |
Logical negation |
\lnot |
¬ |
U+00AC |
 |
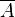 |
\bar |
|
U+0305 |
Quantifiers
Deduction symbols
| Symbol |
Usage |
Interpretation |
Article |
LaTeX |
HTML |
Unicode |
|---|
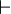 |
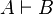 |
Proposition  can be syntactically derived from proposition can be syntactically derived from proposition  |
Propositional calculus |
\vdash |
|
U+22A2 |
 |
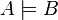 |
Proposition  follows semantically from proposition follows semantically from proposition  |
Inference |
\models |
|
U+22A8 |
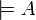 |
Proposition  is universally true is universally true |
Tautology (logic) |
 |
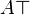 |
\top |
|
U+22A4 |
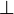 |
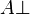 |
Proposition  is contradictory is contradictory |
Contradiction |
\bot |
⊥ |
U+22A5 |
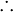 |
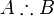 |
Proposition  is true, therefore proposition is true, therefore proposition  is true is true |
Deductive reasoning |
\therefore |
|
U+2234 |
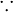 |
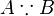 |
Proposition  is true, because is true, because  is true is true |
\because |
|
U+2235 |
 |
|
End of proof |
Q.E.D. |
\blacksquare |
|
U+220E |
 |
\Box |
|
U+25A1 |
See also
References
- Tilo Arens, Frank Hettlich, Christian Karpfinger, Ulrich Kockelkorn, Klaus Lichtenegger, Hellmuth Stachel (2011) (in German), Mathematik (2. ed.), Spektrum Akademischer Verlag, pp. 1483ff., ISBN 3-827-42347-3
- Wolfgang Hackbusch (2010) (in German), Taschenbuch der Mathematik, Band 1 (3. ed.), Springer, pp. 1275ff., ISBN 3-835-10123-4
- Deutsches Institut für Normung: DIN 1302: Allgemeine mathematische Zeichen und Begriffe, Beuth-Verlag, 1999.
- Deutsches Institut für Normung: DIN 1303: Vektoren, Matrizen, Tensoren; Zeichen und Begriffe, Beuth-Verlag, 1987.
- International Standards Organisation: DIN EN ISO 80000-2: Größen und Einheiten – Teil 2: Mathematische Zeichen für Naturwissenschaft und Technik, 2013.
Note: This article is a translation of the German Wikipedia article de:Liste mathematischer Symbole.
External links

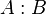
 is defined by
is defined by 
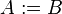
 is defined as equal to
is defined as equal to 
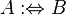
 is defined as equivalent to
is defined as equivalent to 

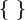
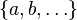
 and so on
and so on
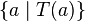
 , that satisfy the condition
, that satisfy the condition 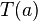

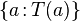

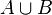
 and
and 

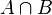
 and
and 
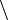
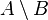
 and
and 

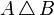
 and
and 

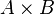
 and
and 
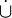
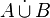
 and
and 


 and
and 
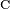
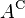


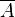
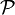
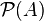

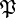
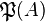
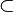

 is a proper subset of
is a proper subset of 

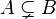


 is a subset of
is a subset of 

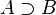
 is a proper superset of
is a proper superset of 
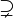
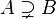
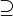

 is a superset of
is a superset of 


 is in the set
is in the set 
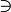
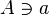
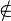
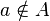
 is not in the set
is not in the set 
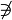
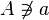
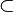 and
and  are used inconsistently and often do not exclude the equality of the two quantities.
are used inconsistently and often do not exclude the equality of the two quantities.


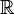
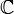
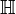

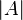


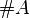

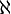
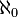 ,
, 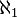 , ...
, ...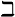
 ,
,  , ...
, ...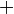

 added to
added to 

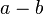
 subtracted from
subtracted from 

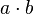
 multiplied by
multiplied by 



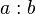
 divided by
divided by 
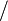

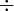





 or the additive inverse of
or the additive inverse of 
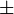
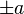

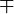
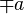

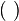
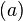
 is evaluated first
is evaluated first![[~]](../I/m/8fd6f25a2c5baf0b452ad209974c725c.png)
![[a]](../I/m/88164354652817ffee36d596a683a2d4.png)

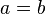
 equals
equals 


 does not equal
does not equal 


 is identical to
is identical to 
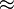
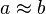
 is approximately equal to
is approximately equal to 

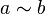
 is proportional to
is proportional to 
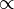
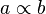
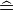
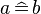
 corresponds to
corresponds to 


 is less than
is less than 
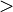
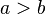
 is greater than
is greater than 

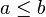
 is less than or equal to
is less than or equal to 
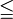
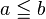
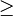
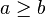
 is greater than or equal to
is greater than or equal to 
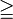
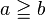

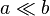
 is much smaller than
is much smaller than 
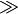
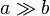
 is much bigger than
is much bigger than 

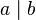
 divides
divides 
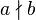
 does not divide
does not divide 

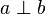
 and
and  are relatively prime
are relatively prime

 and
and 
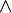
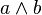


 and
and 

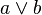

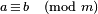
 and
and  are congruent modulo
are congruent modulo 
![[~~]](../I/m/cac765c5f200573ea4d7eba350e4c607.png)
![[a,b]](../I/m/2c3d331bc98b44e71cb2aae9edadca7e.png)
 and
and 
![]~~[](../I/m/7d22940947547c5e4be72378b1bd38e5.png)
![]a,b[](../I/m/e46b2a760c57eb995b62bd166b835b1e.png)
 and
and 
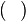
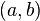

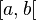
 and
and 
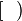
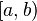
![]~~]](../I/m/d3847530971a7bed5d94340aceccc821.png)
![]a,b]](../I/m/eeac36b17358aa3ca5516b59003d1560.png)
 and
and 
![(~~]](../I/m/d05afd0f1d6d3c620335ad29ff676fd3.png)
![(a,b]](../I/m/a33b8ca44ded30abf82b7dca332e9a96.png)

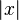

![\left[ ~~ \right]](../I/m/e10fc02cad552ee3fcfaee4e52ab6bec.png)
![\left[ x \right]](../I/m/4fcbf9b418b2ad4ef36169fb15a32bdd.png)






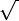
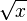

![\sqrt[n]{x}](../I/m/5e4352778f3b156f05ef056f9793ec36.png)
 -th root of
-th root of 
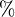
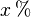
 percent
percent
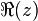
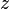
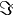
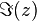
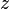


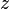

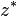

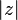
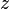
 and
and 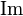 .
.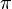


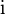
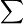
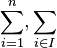
 to
to  or over all elements
or over all elements  in set
in set 

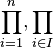
 to
to  or over all elements
or over all elements  in set
in set 
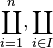
 to
to  or over all elements
or over all elements  in set
in set 
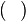

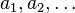
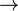

 tends to limit
tends to limit 
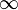
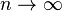
 tends to infinity
tends to infinity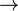

 maps from set
maps from set  to set
to set 
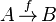

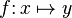
 maps element
maps element  to element
to element 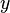
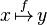
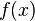
 under function
under function 
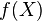
 under function
under function 
![[ ~~ ]](../I/m/cac765c5f200573ea4d7eba350e4c607.png)
![f[X]](../I/m/6b906c857a0e638ba5fb197345117b28.png)
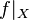
 to set
to set 

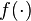

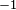
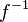



 and
and 

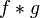
 and
and 




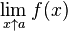
 as
as  approaches
approaches  from below
from below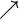
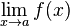
 as
as  approaches
approaches 
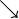
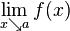
 as
as  approaches
approaches  from above
from above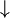
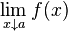


 is asymptotically equal to function
is asymptotically equal to function 

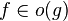
 grows slower than
grows slower than 

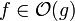
 grows not substantially faster than
grows not substantially faster than 
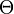
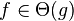
 grows as fast as
grows as fast as 

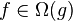
 grows not substantially slower than
grows not substantially slower than 
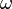
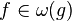
 grows faster than
grows faster than 

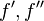


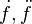
 with respect to time (in physics)
with respect to time (in physics)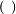

 -th derivative of function
-th derivative of function 
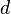
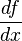
 with respect to variable
with respect to variable 


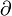
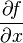
 with respect to variable
with respect to variable 

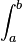 ,
, 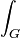
 and
and  or over set
or over set 
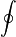
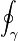
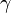
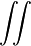
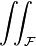

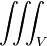


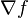

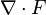
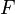
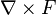
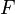
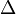
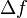


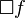

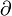
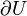
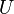

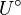
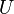

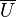
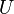

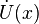
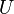 of point
of point 




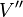





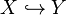
 into
into 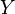
![[~~]](../I/m/cac765c5f200573ea4d7eba350e4c607.png)
![[AB]](../I/m/5e32d4dbe98ef3af1b5123ccba43cbf7.png)
 and
and 

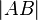
 and
and 

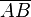
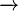
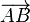
 and
and 
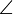
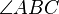
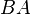 and
and 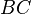

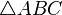
 ,
,  and
and 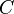

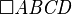
 ,
,  ,
, 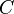 and
and 
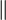
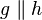
 and
and  are parallel
are parallel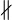
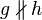
 and
and  are not parallel
are not parallel
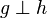
 and
and  are orthogonal
are orthogonal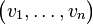
 through
through 

 through
through 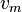
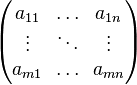
 through
through 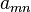

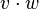
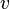 and
and 
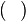
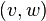
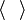
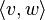
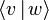

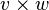
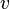 and
and 
![[~~]](../I/m/cac765c5f200573ea4d7eba350e4c607.png)
![[v,w]](../I/m/8820ef1eb7856a10b6bf90f90360cb0d.png)
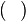

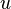 ,
, 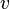 and
and 
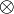
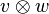
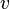 and
and 
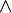

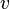 and
and 

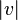
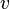


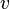

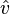
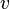

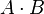
 and
and 

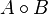
 and
and 
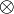

 and
and 
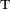
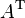

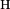
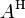



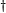
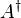
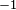


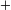
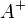


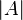


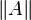

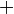
 and
and 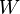


 and
and 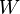

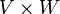
 and
and 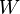
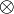
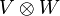
 and
and 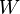
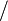
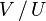
 by subspace
by subspace 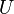
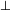
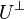
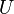

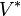


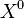

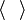



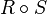
 and
and 
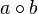
 and
and  (general)
(general)
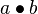

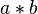

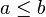
 and
and 

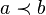
 is a predecessor of element
is a predecessor of element 
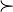
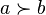
 is a successor of element
is a successor of element 

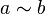
 and
and 
![[ ~~ ]](../I/m/cac765c5f200573ea4d7eba350e4c607.png)
![[ a ]](../I/m/88164354652817ffee36d596a683a2d4.png)

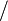
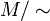
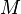 by equivalence relation
by equivalence relation 
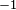
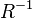

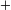
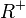


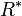


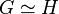
 and
and 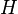 are isomorphic
are isomorphic
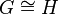

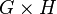
 and
and 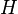

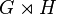
 and
and 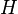
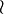
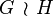
 and
and 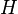

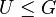
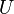 is a subgroup of group
is a subgroup of group 

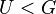
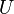 is a proper subgroup of group
is a proper subgroup of group 
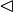
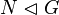
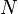 is a normal subgroup of group
is a normal subgroup of group 
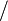

 by normal subgroup
by normal subgroup 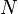

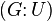
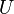 in group
in group 
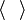
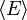
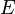
![[ ~~ ]](../I/m/cac765c5f200573ea4d7eba350e4c607.png)
![[ g, h ]](../I/m/96c5245a708de7bd96289e21b83f0bcf.png)
 and
and 
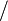
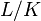
 over field
over field 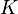

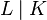

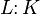
![[ L \colon K ]](../I/m/bc6615c053aef2d3b1d21c53c0df55d6.png)
 over
over 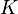


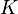

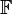

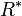



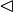
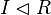
 is an ideal of ring
is an ideal of ring 
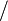
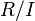
 by ideal
by ideal 
![[ ~~ ]](../I/m/cac765c5f200573ea4d7eba350e4c607.png)
![R[ X ]](../I/m/bc7fa5ab3a6d56e03880fba0532b0eca.png)
 with variable
with variable 
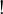

 elements
elements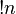
 elements (permutations without fixed points)
elements (permutations without fixed points)
 odd)
odd)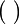

 -combinations of
-combinations of  elements without repetition
elements without repetition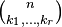
 elements of which
elements of which 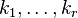 are identical
are identical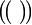
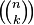
 -combinations of
-combinations of  elements with repetition
elements with repetition
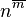
 with
with  factors
factors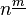
 with
with  factors
factors
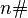






 given event
given event 
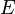



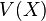

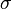
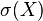

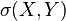
 and
and 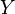

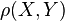
 and
and 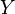

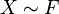
 has distribution
has distribution 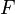
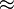
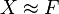
 has distribution
has distribution 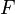 approximately
approximately
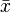

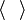

 (in physics)
(in physics)


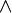

 and proposition
and proposition 
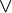

 or proposition
or proposition  (or both)
(or both)

 follows from proposition
follows from proposition  and vice versa
and vice versa
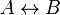

 follows proposition
follows proposition 


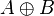
 or proposition
or proposition 
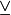
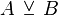
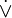
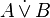

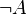


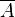

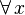


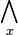

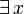
 exists
exists
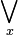
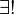
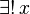
 exists
exists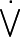
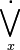
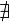
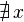
 exists
exists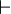
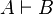
 can be syntactically derived from proposition
can be syntactically derived from proposition 

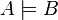
 follows semantically from proposition
follows semantically from proposition 
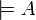
 is universally true
is universally true
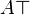
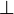
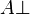
 is contradictory
is contradictory
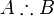
 is true, therefore proposition
is true, therefore proposition  is true
is true
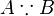
 is true, because
is true, because  is true
is true
