List of Maths formulae involving π
| Part of a series of articles on the |
| mathematical constant π |
|---|
 |
| Uses |
| Properties |
| Value |
| People |
| History |
| In culture |
| Related topics |
The following is a list of significant formulae involving the mathematical constant π. The list contains only formulae whose significance is established either in the article on the formula itself, the article Pi, or the article Approximations of π.
Classical geometry
where C is the circumference of a circle, d is the diameter.
where A is the area of a circle and r is the radius.
where V is the volume of a sphere and r is the radius.
where SA is the surface area of a sphere and r is the radius.
Physics
- Coulomb's law for the electric force:
- Period of a simple pendulum with small amplitude:
- The buckling formula:
Formulae yielding π
Integrals
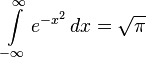 (see Gaussian integral).
(see Gaussian integral).
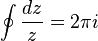 (when the path of integration winds once counterclockwise around 0. See also Cauchy's integral formula)
(when the path of integration winds once counterclockwise around 0. See also Cauchy's integral formula)
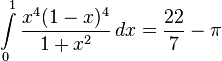 (see also Proof that 22/7 exceeds π).
(see also Proof that 22/7 exceeds π).
Efficient infinite series
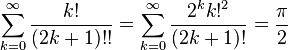 (see also Double factorial)
(see also Double factorial)
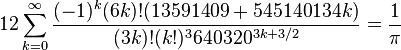 (see Chudnovsky algorithm)
(see Chudnovsky algorithm)
The following are efficient for calculating arbitrary binary digits of π:
Other infinite series
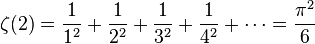 (see also Basel problem and Riemann zeta function)
(see also Basel problem and Riemann zeta function)
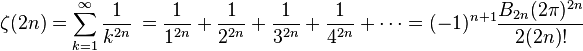 , where B2n is a Bernoulli number.
, where B2n is a Bernoulli number.
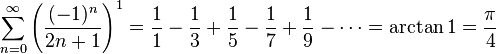 (see Leibniz formula for pi)
(see Leibniz formula for pi)
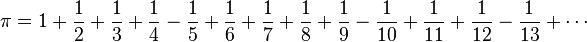 (Euler, 1748)
(Euler, 1748)
- After the first two terms, the signs are determined as follows: If the denominator is a prime of the form 4m - 1, the sign is positive; if the denominator is a prime of the form 4m + 1, the sign is negative; for composite numbers, the sign is equal the product of the signs of its factors.[3]
Machin-like formulae
See also Machin-like formula.
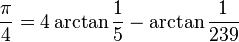 (the original Machin's formula)
(the original Machin's formula)
where  is the n'th Fibonacci number.
is the n'th Fibonacci number.
Infinite series
Some infinite series involving pi are:[4]
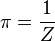 | 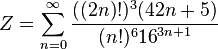 |
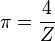 | 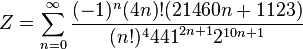 |
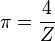 | 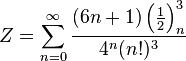 |
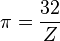 | 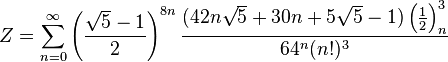 |
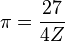 | 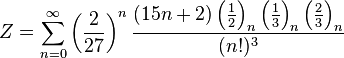 |
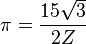 | 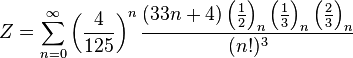 |
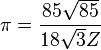 | 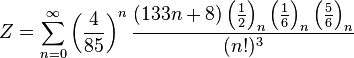 |
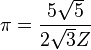 | 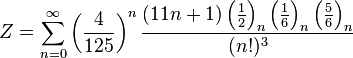 |
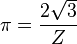 | 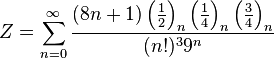 |
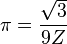 | 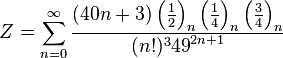 |
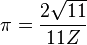 | 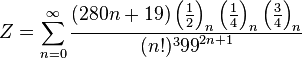 |
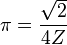 | 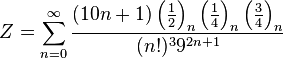 |
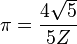 | 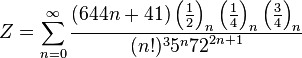 |
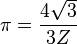 | 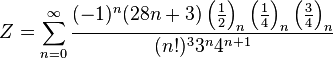 |
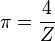 | 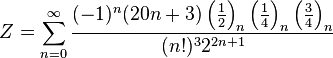 |
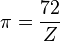 | 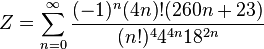 |
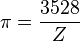 | 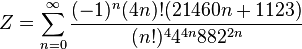 |
where
is the Pochhammer symbol for the falling factorial. See also Ramanujan–Sato series.
Infinite products
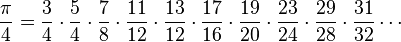 (Euler)
(Euler)- where the numerators are the odd primes; each denominator is the multiple of four nearest to the numerator.
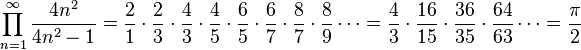 (see also Wallis product)
(see also Wallis product)
Vieta's formula:
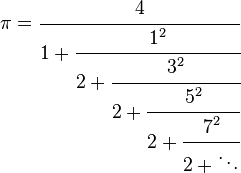
Three continued fractions
For more on this third identity, see Euler's continued fraction formula.
(See also Continued fraction and Generalized continued fraction.)
Miscellaneous
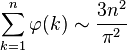 (see Euler's totient function)
(see Euler's totient function)
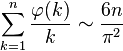 (see Euler's totient function)
(see Euler's totient function)
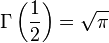 (see also Gamma function)
(see also Gamma function)
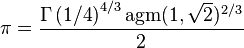 (where agm is the arithmetic-geometric mean)
(where agm is the arithmetic-geometric mean)
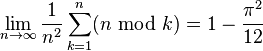 (where mod is the modulo function which gives the rest of a division this formula is getting better for higher n)
(where mod is the modulo function which gives the rest of a division this formula is getting better for higher n)
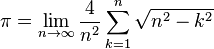 (Riemann sum to evaluate the area of the unit circle)
(Riemann sum to evaluate the area of the unit circle)
See also
References
- ↑ Cetin Hakimoglu-Brown Derivation of Rapidly Converging Infinite Series
- ↑ Weisstein, Eric W. "Pi Formulas", MathWorld
- ↑ Carl B. Boyer, A History of Mathematics, Chapter 21., p. 488-489
- ↑ Simon Plouffe / David Bailey. "The world of Pi". Pi314.net. Retrieved 2011-01-29.
"Collection of series for π". Numbers.computation.free.fr. Retrieved 2011-01-29.
Further reading
- Peter Borwein, The Amazing Number Pi
- Kazuya Kato, Nobushige Kurokawa, Saito Takeshi: Number Theory 1: Fermat's Dream. American Mathematical Society, Providence 1993, ISBN 0-8218-0863-X.
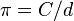
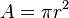
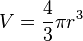
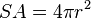
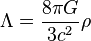
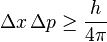
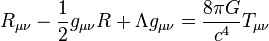
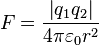
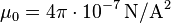
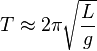
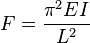
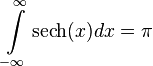
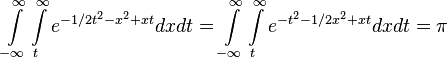
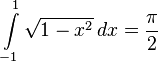
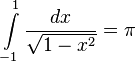
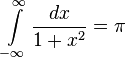 (integral form of
(integral form of 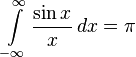
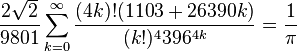 (see
(see 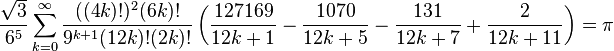
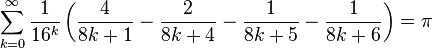 (see
(see 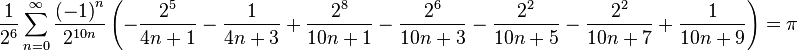
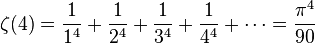
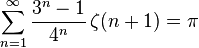
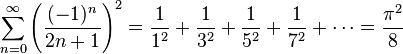
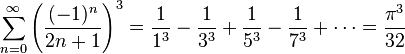
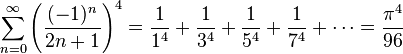
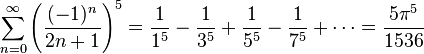
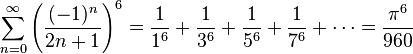
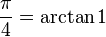
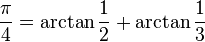
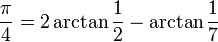
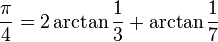
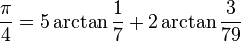

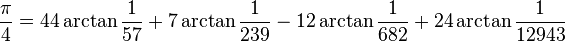
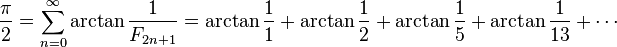
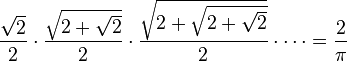
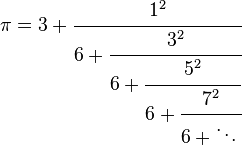
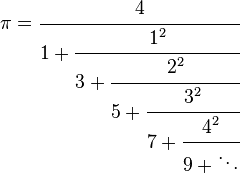
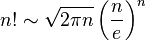 (
(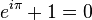 (
(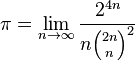 (by
(by