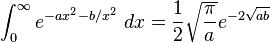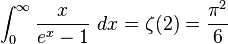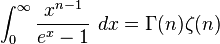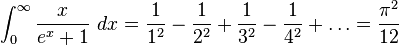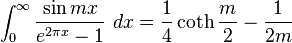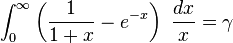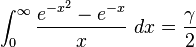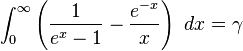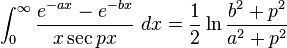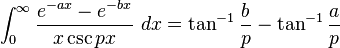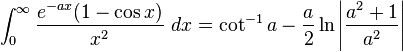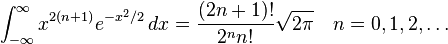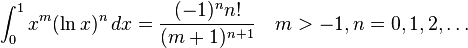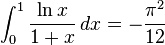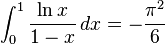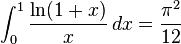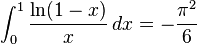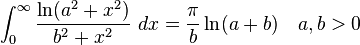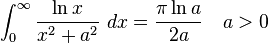List of definite integrals
| Part of a series of articles about | ||||||
| Calculus | ||||||
|---|---|---|---|---|---|---|
|
||||||
|
Specialized |
||||||
In mathematics, the definite integral:
is the area of the region in the xy-plane bounded by the graph of f, the x-axis, and the lines x = a and x = b, such that area above the x-axis adds to the total, and that below the x-axis subtracts from the total.
The fundamental theorem of calculus establishes the relationship between indefinite and definite integrals and introduces a technique for evaluating definite integrals.
If the interval is infinite the definite integral is called an improper integral and defined by using appropriate limiting procedures. for example:
The following is a list of the most common definite Integrals. For a list of indefinite integrals see List of indefinite integrals
Definite integrals involving rational or irrational expression
Definite integrals involving trigonometric functions
-
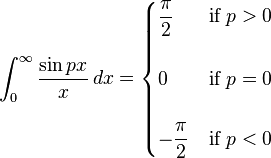 (see Dirichlet integral)
(see Dirichlet integral)
Definite integrals involving exponential functions
Definite integrals involving logarithmic functions
Definite integrals involving hyperbolic functions
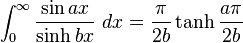
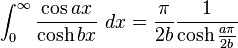
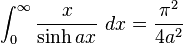
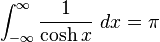
Miscellaneous definite integrals
![\int_{0}^{\infty }\frac{f(ax)-f(bx)}{x}\ dx=[{f(0)-f(\infty)}]\ln \frac{b}{a}](../I/m/d7ae72ffa220c46691c700fa45f12567.png)
See also
References
[1] [2]; -webkit-column-width: refs [3] [1] [2]; column-width: refs [3] [1] [2]; list-style-type: decimal;">
- 1 2 3 Zwillinger, Daniel (2003). CRC standard mathematical tables and formulae (32nd ed.). CRC Press. ISBN 978-1439835487.
- 1 2 3 Abramowitz, Milton; Stegun, Irene A. (1965). Handbook of mathematical functions with formulas, graphs, and mathematical tables (Unabridged and unaltered republ. [der Ausg.] 1964, 5. Dover printing ed.). U.S. Govt. Print. Off. ISBN 978-0486612720.
- 1 2 Murray R. Spiegel, Seymour Lipschutz, John Liu (2009). Mathematical handbook of formulas and tables (3rd ed.). McGraw-Hill. ISBN 978-0071548557.
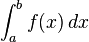
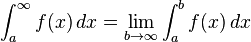
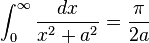
![\int_0^\infty \frac{x^{m}dx}{x^{n}+a^{n}}=\frac{\pi a^{m-n+1}}{n \sin [(m+1)(\pi /n)]} ,0<m+1<n](../I/m/f2703ce76186c3e1e735a42c38e49d76.png)
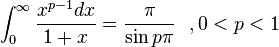
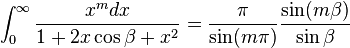
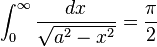
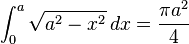
![\int_0^a x^m (a^n-x^n)^p\,dx=\frac{a^{m+1+np}\Gamma [(m+1)/n]\Gamma(p+1)}{n\Gamma [((m+1)/n)+p+1]}](../I/m/69aa0e07dd2e301369691a9998af3586.png)
![\int_0^\infty \frac{x^m \, dx}{({x^n+a^n)}^r}=\frac{(-1)^{r-1}\pi a^{m+1-nr}\Gamma [(m+1)/n]}{n\sin[(m+1)\pi/n](r-1)!\Gamma[(m+1)/n-r+1]} \ \ , n(r-2)<m+1<nr](../I/m/8b5405f0abdd8cac8382e8be01cba608.png)
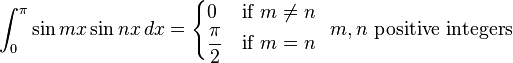
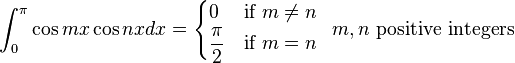
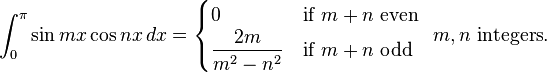
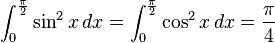
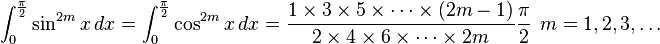
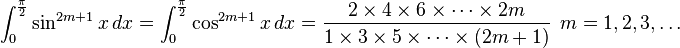
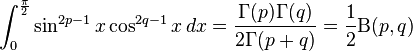
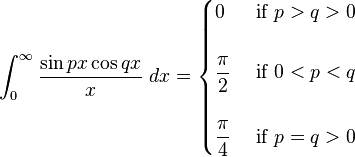
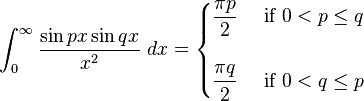
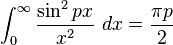
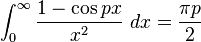
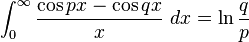
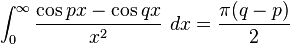
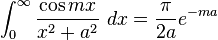
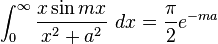
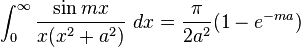
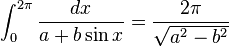
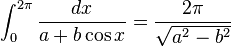
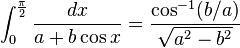
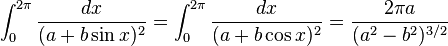
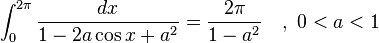
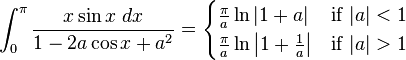
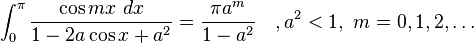
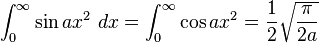
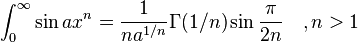
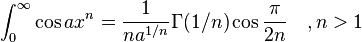
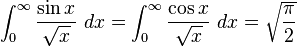
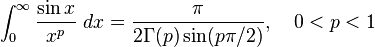
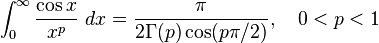
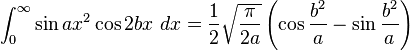
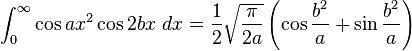
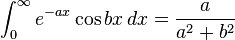
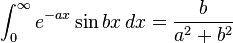
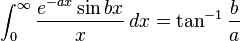
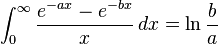
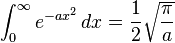
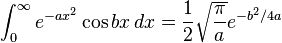
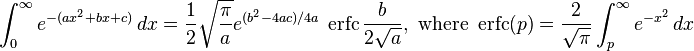
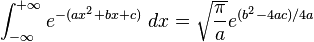
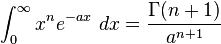
![\int_0^\infty x^{m}e^{-ax^2}\ dx=\frac{\Gamma [(m+1)/2]}{2a^{(m+1)/2}}](../I/m/36829d976e34d1ed1e8f22f5ad237a75.png)