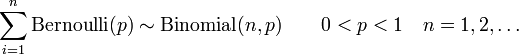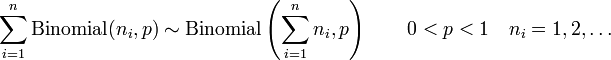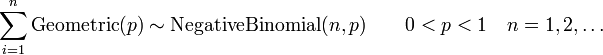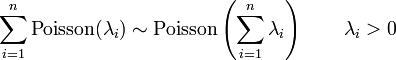List of convolutions of probability distributions

In probability theory, the probability distribution of the sum of two or more independent random variables is the convolution of their individual distributions. The term is motivated by the fact that the probability mass function or probability density function of a sum of random variables is the convolution of their corresponding probability mass functions or probability density functions respectively. Many well known distributions have simple convolutions. The following is a list of these convolutions. Each statement is of the form

\sum_{i=1}^n X_i \sim Y

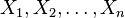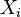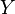where $X_1, X_2,\dots, X_n\,$ are independent and identically distributed random variables. In place of $X_i$ and $Y$ the names of the corresponding distributions and their parameters have been indicated.

Discrete distributions

$\sum_{i=1}^n \mathrm{Bernoulli}(p) \sim \mathrm{Binomial}(n,p) \qquad 0<p<1 \quad n=1,2,\dots \,\!$
$\sum_{i=1}^n \mathrm{Binomial}(n_i,p) \sim \mathrm{Binomial}\left(\sum_{i=1}^n n_i,p\right) \qquad 0<p<1 \quad n_i=1,2,\dots \,\!$
$\sum_{i=1}^n \mathrm{NegativeBinomial}(n_i,p) \sim \mathrm{NegativeBinomial}\left(\sum_{i=1}^n n_i,p\right) \qquad 0<p<1 \quad n_i=1,2,\dots \,\!$
$\sum_{i=1}^n \mathrm{Geometric}(p) \sim \mathrm{NegativeBinomial}(n,p) \qquad 0<p<1 \quad n=1,2,\dots \,\!$
$\sum_{i=1}^n \mathrm{Poisson}(\lambda_i) \sim \mathrm{Poisson}\left(\sum_{i=1}^n \lambda_i\right) \qquad \lambda_i>0 \,\!$

Continuous distributions

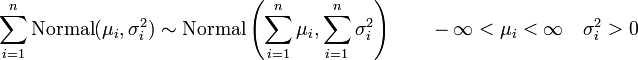
$\sum_{i=1}^n \mathrm{Normal}(\mu_i,\sigma_i^2) \sim \mathrm{Normal}\left(\sum_{i=1}^n \mu_i, \sum_{i=1}^n \sigma_i^2\right) \qquad -\infty<\mu_i<\infty \quad \sigma_i^2>0$
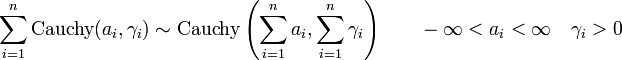
$\sum_{i=1}^n \mathrm{Cauchy}(a_i,\gamma_i) \sim \mathrm{Cauchy}\left(\sum_{i=1}^n a_i, \sum_{i=1}^n \gamma_i\right) \qquad -\infty<a_i<\infty \quad \gamma_i>0$
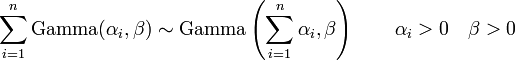
$\sum_{i=1}^n \mathrm{Gamma}(\alpha_i,\beta) \sim \mathrm{Gamma}\left(\sum_{i=1}^n \alpha_i,\beta\right) \qquad \alpha_i>0 \quad \beta>0$
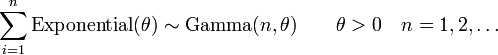
$\sum_{i=1}^n \mathrm{Exponential}(\theta) \sim \mathrm{Gamma}(n,\theta) \qquad \theta>0 \quad n=1,2,\dots$
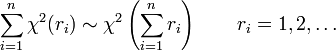
$\sum_{i=1}^n \chi^2(r_i) \sim \chi^2\left(\sum_{i=1}^n r_i\right) \qquad r_i=1,2,\dots$
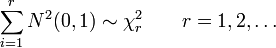
$\sum_{i=1}^r N^2(0,1) \sim \chi^2_r \qquad r=1,2,\dots$
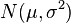$\sum_{i=1}^n(X_i - \bar X)^2 \sim \sigma^2 \chi^2_{n-1}, \quad$ where $X_1,\dots,X_n$ is a random sample from $N(\mu,\sigma^2)$ and $\bar X = \frac{1}{n} \sum_{i=1}^n X_i. \,\!$

References

Hogg, Robert V.; McKean, Joseph W.; Craig, Allen T. (2004). Introduction to mathematical statistics (6th ed.). Upper Saddle River, New Jersey: Prentice Hall. p. 692. ISBN 978-0-13-008507-8. MR 467974.

This article is issued from Wikipedia - version of the Saturday, February 28, 2015. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.

List of convolutions of probability distributions

Discrete distributions

Continuous distributions

See also

References