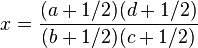Linkage disequilibrium
In population genetics, linkage disequilibrium is the non-random association of alleles at different loci i.e. the presence of statistical associations between alleles at different loci that are different from what would be expected if alleles were independently, randomly sampled based on their individual allele frequencies.[1] If there is no linkage disequilibrium between alleles at different loci they are said to be in linkage equilibrium.
Linkage disequilibrium is influenced by many factors, including selection, the rate of recombination, the rate of mutation, genetic drift, the system of mating, population structure, and genetic linkage. As a result, the pattern of linkage disequilibrium in a genome is a powerful signal of the population genetic forces that are structuring it.
In spite of its name, linkage disequilibrium may exist between alleles at different loci without any genetic linkage between them and independently of whether or not allele frequencies are in equilibrium (not changing with time).[1] Furthermore, linkage disequilibrium is sometimes referred to as gametic phase disequilibrium;[2] however, the concept also applies to asexual organisms and therefore does not depend on the presence of gametes.
Formal Definition
Suppose that among the gametes that are formed in a sexually reproducing population, allele A occurs with frequency 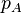 at one locus (i.e.
at one locus (i.e. 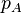 is the proportion of gametes with A at the first locus), while at a different locus allele B occurs with frequency
is the proportion of gametes with A at the first locus), while at a different locus allele B occurs with frequency 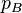 . Similarly, let
. Similarly, let 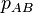 be the frequency of A and B occurring together in the same gamete (i.e.
be the frequency of A and B occurring together in the same gamete (i.e. 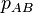 is the frequency of the AB haplotype).
is the frequency of the AB haplotype).
The association between the alleles A and B can be regarded as completely random when the probability of A and B occurring together in a randomly selected gamete 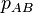 is just the probability that A and B independently occur in the same gamete, which is given by
is just the probability that A and B independently occur in the same gamete, which is given by 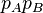 . If
. If 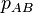 differs from
differs from 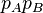 for any reason, then there is non-random association between A and B and we say that there is linkage disequilibrium between these alleles.
for any reason, then there is non-random association between A and B and we say that there is linkage disequilibrium between these alleles.
The level of linkage disequilibrium between A and B can be quantified by the coefficient of linkage disequilibrium 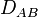 , which is defined as
, which is defined as
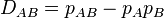 . . |
Linkage disequilibrium corresponds to 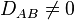 . In the case
. In the case 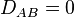 we have
we have  and the alleles A and B are said to be in linkage equilibrium. The subscript AB on
and the alleles A and B are said to be in linkage equilibrium. The subscript AB on 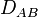 emphasizes that it is a property of the alleles A and B. Different alleles at the same loci may have different coefficients of linkage disequilibrium.
emphasizes that it is a property of the alleles A and B. Different alleles at the same loci may have different coefficients of linkage disequilibrium.
Linkage disequilibrium can be defined in a similar way for asexual populations using population allele frequencies. Furthermore, it is also possible to define linkage disequilibrium between three or more alleles, however these higher order associations are not commonly used in practice.[1]
Measures of linkage disequilibrium derived from 
The coefficient of linkage disequilibrium  is not always a convenient measure of linkage disequilibrium because its range of possible values depends on the frequencies of the alleles it refers to. This makes it difficult to compare the level of linkage disequilibrium between different pairs of alleles.
is not always a convenient measure of linkage disequilibrium because its range of possible values depends on the frequencies of the alleles it refers to. This makes it difficult to compare the level of linkage disequilibrium between different pairs of alleles.
Lewontin[3] suggested normalising D by dividing it by the theoretical maximum for the observed allele frequencies as follows:
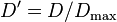 |
where
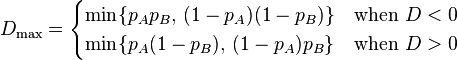 |
An alternative to 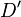 is the correlation coefficient between pairs of loci, expressed as
is the correlation coefficient between pairs of loci, expressed as
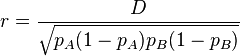 .
.
Example: Two-loci and two-alleles
Consider the haplotypes for two loci A and B with two alleles each—a two-locus, two-allele model. Then the following table defines the frequencies of each combination:
| Haplotype | Frequency |
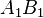 | 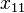 |
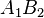 | 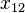 |
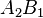 | 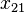 |
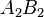 | 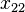 |
Note that these are relative frequencies. One can use the above frequencies to determine the frequency of each of the alleles:
| Allele | Frequency |
 | 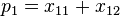 |
 | 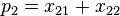 |
 | 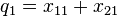 |
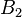 | 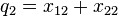 |
If the two loci and the alleles are independent from each other, then one can express the observation 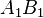 as "
as " is found and
is found and 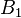 is found". The table above lists the frequencies for
is found". The table above lists the frequencies for  ,
,  , and for
, and for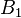 ,
, 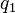 , hence the frequency of
, hence the frequency of 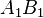 is
is 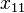 , and according to the rules of elementary statistics
, and according to the rules of elementary statistics  .
.
The deviation of the observed frequency of a haplotype from the expected is a quantity[4] called the linkage disequilibrium[5] and is commonly denoted by a capital D:
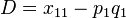 |
The following table illustrates the relationship between the haplotype frequencies and allele frequencies and D.
 |  | Total | |
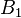 | 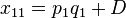 |  | 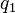 |
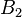 | 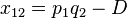 | 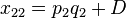 | 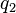 |
| Total |  |  |  |
Role of recombination
In the absence of evolutionary forces other than random mating, Mendelian segregation, random chromosomal assortment, and chromosomal crossover (i.e. in the absence of natural selection, inbreeding, and genetic drift),
the linkage disequilibrium measure  converges to zero along the time axis at a rate
depending on the magnitude of the recombination rate
converges to zero along the time axis at a rate
depending on the magnitude of the recombination rate  between the two loci.
between the two loci.
Using the notation above, 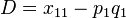 , we can demonstrate this convergence to zero
as follows. In the next generation,
, we can demonstrate this convergence to zero
as follows. In the next generation, 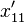 , the frequency of the haplotype
, the frequency of the haplotype 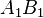 , becomes
, becomes
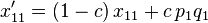 |
This follows because a fraction 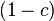 of the haplotypes in the offspring have not
recombined, and are thus copies of a random haplotype in their parents. A fraction
of the haplotypes in the offspring have not
recombined, and are thus copies of a random haplotype in their parents. A fraction 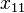 of those are
of those are 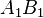 . A fraction
. A fraction  have recombined these two loci. If the parents result from random mating, the probability of the
copy at locus
have recombined these two loci. If the parents result from random mating, the probability of the
copy at locus  having allele
having allele  is
is  and the probability
of the copy at locus
and the probability
of the copy at locus  having allele
having allele 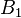 is
is 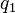 , and as these copies are initially in the two different gametes that formed the diploid genotype, these are independent events so that the probabilities can be multiplied.
, and as these copies are initially in the two different gametes that formed the diploid genotype, these are independent events so that the probabilities can be multiplied.
This formula can be rewritten as
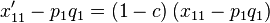 |
so that
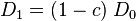 |
where  at the
at the  -th generation is designated as
-th generation is designated as 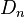 . Thus we have
. Thus we have
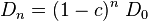 . . |
If 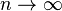 , then
, then 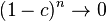 so that
so that 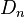 converges to zero.
converges to zero.
If at some time we observe linkage disequilibrium, it will disappear in the future due to recombination. However, the smaller the distance between the two loci, the smaller will be the rate of convergence of  to zero.
to zero.
Example: Human Leukocyte Antigen (HLA) alleles
HLA constitutes a group of cell surface antigens as MHC of humans. Because HLA genes are located at adjacent loci on the particular region of a chromosome and presumed to exhibit epistasis with each other or with other genes, a sizable fraction of alleles are in linkage disequilibrium.
An example of such linkage disequilibrium is between HLA-A1 and B8 alleles in unrelated Danes[6] referred to by Vogel and Motulsky (1997).[7]
| Antigen j | Total | ||||
|---|---|---|---|---|---|
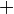 |
 | ||||
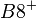 |
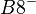 | ||||
| Antigen i | 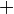 |
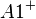 |
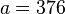 |
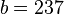 |
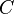 |
 |
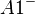 |
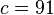 |
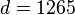 |
 | |
| Total |  |
 |
 | ||
| No. of individuals | |||||
Because HLA is codominant and HLA expression is only tested locus by locus in surveys, LD measure is to be estimated from such a 2x2 table to the right.[7][8][9][10]
expression (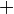 ) frequency of antigen
) frequency of antigen  :
:
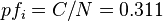 ;
;
expression (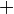 ) frequency of antigen
) frequency of antigen 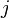 :
:
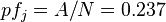 ;
;
frequency of gene  :
:
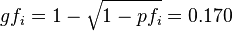 ,
,
and
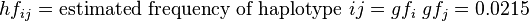 .
.
Denoting the '―' alleles at antigen i to be 'x,' and at antigen j to be 'y,' the observed frequency of haplotype xy is
and the estimated frequency of haplotype xy is
![e[hf_{xy}]=\sqrt{(D/N)(B/N)}](../I/m/91ddb326cdaec8f509cd491e844bdb2f.png) .
.
Then LD measure 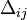 is expressed as
is expressed as
![\Delta_{ij}=o[hf_{xy}]-e[hf_{xy}]=\frac{\sqrt{Nd}-\sqrt{BD}}{N}=0.0769](../I/m/20a9e461731aefbcc952833c8ef8f306.png) .
.
Standard errors 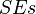 are obtained as follows:
are obtained as follows:
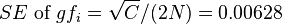 ,
,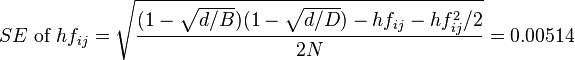
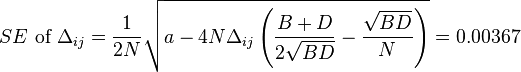 .
.
Then, if
exceeds 2 in its absolute value, the magnitude of 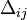 is statistically significantly large. For data in Table 1 it is 20.9, thus existence of statistically significant LD between A1 and B8 in the population is admitted.
is statistically significantly large. For data in Table 1 it is 20.9, thus existence of statistically significant LD between A1 and B8 in the population is admitted.
| HLA-A alleles i | HLA-B alleles j | 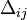 |
 |
|---|---|---|---|
| A1 | B8 | 0.065 | 16.0 |
| A3 | B7 | 0.039 | 10.3 |
| A2 | Bw40 | 0.013 | 4.4 |
| A2 | Bw15 | 0.01 | 3.4 |
| A1 | Bw17 | 0.014 | 5.4 |
| A2 | B18 | 0.006 | 2.2 |
| A2 | Bw35 | -0.009 | -2.3 |
| A29 | B12 | 0.013 | 6.0 |
| A10 | Bw16 | 0.013 | 5.9 |
Table 2 shows some of the combinations of HLA-A and B alleles where significant LD was observed among pan-europeans.[10]
Vogel and Motulsky (1997)[7] argued how long would it take that linkage disequilibrium between loci of HLA-A and B disappeared. Recombination between loci of HLA-A and B was considered to be of the order of magnitude 0.008. We will argue similarly to Vogel and Motulsky below. In case LD measure was observed to be 0.003 in Pan-europeans in the list of Mittal[10] it is mostly non-significant. If 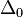 had reduced from 0.07 to 0.003 under recombination effect as shown by
had reduced from 0.07 to 0.003 under recombination effect as shown by 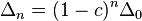 , then
, then 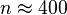 . Suppose a generation took 25 years, this means 10,000 years. The time span seems rather short in the history of humans. Thus observed linkage disequilibrium between HLA-A and B loci might indicate some sort of interactive selection.[7]
. Suppose a generation took 25 years, this means 10,000 years. The time span seems rather short in the history of humans. Thus observed linkage disequilibrium between HLA-A and B loci might indicate some sort of interactive selection.[7]
The presence of linkage disequilibrium between an HLA locus and a presumed major gene of disease susceptibility corresponds to any of the following phenomena:
- Relative risk for the person having a specific HLA allele to become suffered from a particular disease is greater than 1.[11]
- The HLA antigen frequency among patients exceeds more than that among a healthy population. This is evaluated by
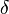 value[12] to exceed 0.
value[12] to exceed 0.
| Ankylosing spondylitis | Total | |||
|---|---|---|---|---|
| Patients | Healthy controls | |||
| HLA alleles | 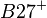 |
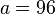 |
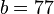 |
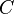 |
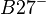 |
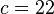 |
 |
 | |
| Total |  |
 |
 | |
- 2x2 association table of patients and healthy controls with HLA alleles shows a significant deviation from the equilibrium state deduced from the marginal frequencies.
(1) Relative risk
Relative risk of an HLA allele for a disease is approximated by the odds ratio in the 2x2 association table of the allele with the disease. Table 3 shows association of HLA-B27 with ankylosing spondylitis among a Dutch population.[13] Relative risk  of this allele is approximated by
of this allele is approximated by
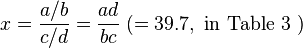 .
.
Woolf's method[14] is applied to see if there is statistical significance. Let
and
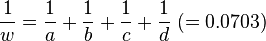 .
.
Then
follows the chi-square distribution with 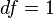 . In the data of Table 3, the significant association exists at the 0.1% level. Haldane's[15] modification applies to the case when either of
. In the data of Table 3, the significant association exists at the 0.1% level. Haldane's[15] modification applies to the case when either of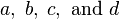 is zero, where replace
is zero, where replace  and
and 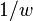 with
with
and
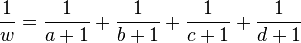 ,
,
respectively.
| Disease | HLA allele | Relative risk (%) | FAD (%) | FAP (%) | 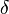 |
|---|---|---|---|---|---|
| Ankylosing spondylitis | B27 | 90 | 90 | 8 | 0.89 |
| Reactive arthritis | B27 | 40 | 70 | 8 | 0.67 |
| Spondylitis in inflammatory bowel disease | B27 | 10 | 50 | 8 | 0.46 |
| Rheumatoid arthritis | DR4 | 6 | 70 | 30 | 0.57 |
| Systemic lupus erythematosus | DR3 | 3 | 45 | 20 | 0.31 |
| Multiple sclerosis | DR2 | 4 | 60 | 20 | 0.5 |
| Diabetes mellitus type 1 | DR4 | 6 | 75 | 30 | 0.64 |
In Table 4, some examples of association between HLA alleles and diseases are presented.[11]
(1a) Allele frequency excess among patients over controls
Even high relative risks between HLA alleles and the diseases were observed, only the magnitude of relative risk would not be able to determine the strength of association.[12] value is expressed by
value is expressed by
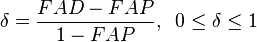 ,
,
where 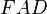 and
and 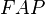 are HLA allele frequencies among patients and healthy populations, respectively.[12] In Table 4,
are HLA allele frequencies among patients and healthy populations, respectively.[12] In Table 4, 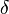 column was added in this quotation. Putting aside 2 diseases with high relative risks both of which are also with high
column was added in this quotation. Putting aside 2 diseases with high relative risks both of which are also with high 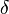 values, among other diseases, juvenile diabetes mellitus (type 1) has a strong association with DR4 even with a low relative risk
values, among other diseases, juvenile diabetes mellitus (type 1) has a strong association with DR4 even with a low relative risk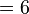 .
.
(2) Discrepancies from expected values from marginal frequencies in 2x2 association table of HLA alleles and disease
This can be confirmed by  test calculating
test calculating
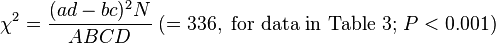 .
.
where 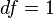 . For data with small sample size, such as no marginal total is greater than 15 (and consequently
. For data with small sample size, such as no marginal total is greater than 15 (and consequently 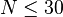 ), one should utilize Yates's correction for continuity or Fisher's exact test.[16]
), one should utilize Yates's correction for continuity or Fisher's exact test.[16]
Resources
A comparison of different measures of LD is provided by Devlin & Risch [17]
The International HapMap Project enables the study of LD in human populations online. The Ensembl project integrates HapMap data with other genetic information from dbSNP.
Analysis software
- PLINK - whole genome association analysis toolset, which can calculate LD among other things
- LDHat
- Haploview
- LdCompare[18]— open-source software for calculating LD.
- SNP and Variation Suite- commercial software with interactive LD plot.
- GOLD - Graphical Overview of Linkage Disequilibrium
- TASSEL -software to evaluate linkage disequilibrium, traits associations, and evolutionary patterns
- rAggr - finds proxy markers (SNPs and indels) that are in linkage disequilibrium with a set of queried markers, using the 1000 Genomes Project and HapMap genotype databases.
Simulation software
See also
- Haploview
- Hardy-Weinberg principle
- Genetic linkage
- Co-adaptation
- Genealogical DNA test
- Tag SNP
- Association Mapping
- Family based QTL mapping
References
- 1 2 3 Slatkin, Montgomery (June 2008). "Linkage disequilibrium — understanding the evolutionary past and mapping the medical future". Nature Reviews Genetics 9 (6): 477–485. doi:10.1038/nrg2361.
- ↑ Falconer, DS; Mackay, TFC (1996). Introduction to Quantitative Genetics (4th ed.). Harlow, Essex, UK: Addison Wesley Longman. ISBN 0-582-24302-5.
- ↑ Lewontin, R. C. (1964). "The interaction of selection and linkage. I. General considerations; heterotic models". Genetics 49 (1): 49–67. PMC 1210557. PMID 17248194.
- ↑ Robbins, R.B. (1 July 1918). "Some applications of mathematics to breeding problems III". Genetics 3 (4): 375–389. PMC 1200443. PMID 17245911.
- ↑ R.C. Lewontin and K. Kojima (1960). "The evolutionary dynamics of complex polymorphisms". Evolution 14 (4): 458–472. doi:10.2307/2405995. ISSN 0014-3820. JSTOR 2405995.
- 1 2 Svejgaard A, Hauge M, Jersild C, Plaz P, Ryder LP, Staub Nielsen L, Thomsen M (1979). The HLA System: An Introductory Survey, 2nd ed. Basel; London; Chichester: Karger; Distributed by Wiley, ISBN 3805530498(pbk).
- 1 2 3 4 Vogel F, Motulsky AG (1997). Human Genetics : Problems and Approaches, 3rd ed.Berlin; London: Springer, ISBN 3-540-60290-9.
- ↑ Mittal KK, Hasegawa T, Ting A, Mickey MR, Terasaki PI (1973). "Genetic variation in the HL-A system between Ainus, Japanese, and Caucasians," In Dausset J, Colombani J, eds. Histocompatibility Testing, 1972, pp. 187-195, Copenhagen: Munksgaard, ISBN 87-16-01101-5.
- ↑ Yasuda N, Tsuji K (1975). "A counting method of maximum likelihood for estimating haplotype frequency in the HL-A system." Jinrui Idengaku Zasshi 20(1): 1-15, PMID 1237691.
- 1 2 3 4 Mittal KK (1976). "The HLA polymorphism and susceptibility to disease." Vox Sang 31: 161-173, PMID 969389.
- 1 2 3 Gregersen PK (2009). "Genetics of rheumatic diseases," InFirestein GS, Budd RC, Harris ED Jr, McInnes IB, Ruddy S, Sergent JS, eds. (2009). Kelley's Textbook of Rheumatology, pp. 305-321, Philadelphia, PA: Saunders/Elsevier, ISBN 978-1-4160-3285-4.
- 1 2 3 Bengtsson BO, Thomson G (1981). "Measuring the strength of associations between HLA antigens and diseases." Tissue Antigens18(5): 356-363, PMID 7344182.
- 1 2 Nijenhuis LE (1977). "Genetic considerations on association between HLA and disease." Hum Genet38(2): 175-182, PMID 908564.
- ↑ Woolf B (1955). "On estimating the relation between blood group and disease." Ann Hum Genet 19(4): 251-253, PMID 14388528.
- ↑ Haldane JB (1956). "The estimation and significance of the logarithm of a ratio of frequencies." Ann Hum Genet20(4): 309-311, PMID 13314400.
- ↑ Sokal RR, Rohlf FJ (1981). Biometry: The Principles and Practice of Statistics in Biological Research. Oxford: W.H. Freeman, ISBN 0-7167-1254-7.
- ↑ Devlin B., Risch N. (1995). "A Comparison of Linkage Disequilibrium Measures for Fine-Scale Mapping" (PDF). Genomics 29 (2): 311–322. doi:10.1006/geno.1995.9003. PMID 8666377.
- ↑ Hao K., Di X., Cawley S. (2007). "LdCompare: rapid computation of single- and multiple-marker r2 and genetic coverage". Bioinformatics 23 (2): 252–254. doi:10.1093/bioinformatics/btl574. PMID 17148510.
Further reading
- Hedrick, Philip W. (2005). Genetics of Populations (3rd ed.). Sudbury, Boston, Toronto, London, Singapore: Jones and Bartlett Publishers. ISBN 0-7637-4772-6.
- Bibliography: Linkage Disequilibrium Analysis : a bibliography of more than one thousand articles on Linkage disequilibrium published since 1918.
| ||||||||||||||||||||||||||||||
![o[hf_{xy}]=\sqrt{d/N}](../I/m/1bac0b997118a0a1a88c724f015eb770.png)
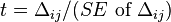
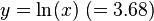
![\chi^2=wy^2\;\left [=193>\chi^2(p=0.001,\; df=1)=10.8 \right ]](../I/m/388430d3c9392e03a17d8f42665f3347.png)