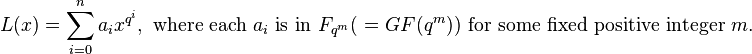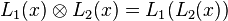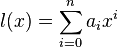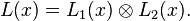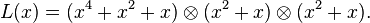Linearised polynomial

In mathematics, a linearised polynomial (or q- polynomial) is a polynomial for which the exponents of all the constituent monomials are powers of q and the coefficients come from some extension field of the finite field of order q.

We write a typical example as

L(x) = \sum_{i=0}^n a_i x^{q^i}, \text{ where each } a_i \text{ is in } F_{q^m} (\text { = } GF(q^m)) \text{ for some fixed positive integer }m.

This special class of polynomials is important from both a theoretical and an applications viewpoint.^[1] The highly structured nature of their roots makes these roots easy to determine.

Properties

The map x → L(x) is a linear map over any field containing F_q
The set of roots of L is an F_q-vector space and is closed under the q-Frobenius map
Conversely, if U is any F_q-linear subspace of some finite field containing F_q, then the polynomial that vanishes exactly on U is a linearised polynomial.
The set of linearised polynomials over a given field is closed under addition and composition of polynomials.
If L is a nonzero linearised polynomial over 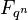$F_{q^n}$ with all of its roots lying in the field 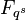$F_{q^s}$ an extension field of 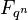$F_{q^n}$ , then each root of L has the same multiplicity, which is either 1, or a positive power of q.^[2]

Symbolic multiplication

In general, the product of two linearised polynomials will not be a linearized polynomial, but since the composition of two linearised polynomials results in a linearised polynomial, composition may be used as a replacement for multiplication and, for this reason, composition is often called symbolic multiplication in this setting. Notationally, if L₁(x) and L₂(x) are linearised polynomials we define

L_1(x) \otimes L_2(x) = L_1(L_2(x))

when this point of view is being taken.

Associated polynomials

The polynomials L(x) and

l(x) = \sum_{i=0}^n a_i x^i \

are q - associates (note: the exponents "qⁱ " of L(x) have been replaced by "i" in l(x)). More specifically, l(x} is called the conventional q-associate of L(x), and L(x) is the linearised q-associate of l(x).

q-polynomials over F_q

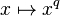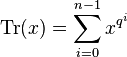Linearised polynomials with coefficients in F_q have additional properties which make it possible to define symbolic division, symbolic reducibility and symbolic factorizaton. Two important examples of this type of linearised polynomial are the Frobenius automorphism $x \mapsto x^q$ and the trace function $\operatorname{Tr}(x) = \sum_{i=0}^{n-1} x^{q^i}$ .

In this special case it can be shown that, as an operation, symbolic multiplication is commutative, associative and distributes over ordinary addition.^[3] Also, in this special case, we can define the operation of symbolic division. If L(x) and L₁(x) are linearised polynomials over F_q, we say that L₁(x) symbolically divides L(x) if there exists a linearised polynomial L₂(x) over F_q for which:

L(x) = L_1(x) \otimes L_2(x).

If L₁(x) and L₂(x) are linearised polynomials over F_q with conventional q-associates l₁(x) and l₂(x) respectively, then L₁(x) symbolically divides L₂(x) if and only if l₁(x) divides l₂(x).^[4] Furthermore, L₁(x) divides L₂(x) in the ordinary sense in this case.^[5]

A linearised polynomial L(x) over F_q of degree > 1 is symbolically irreducible over F_q if the only symbolic decompositions

L(x) = L_1(x) \otimes L_2(x),

with L_i over F_q are those for which one of the factors has degree 1. Note that a symbolically irreducible polynomial is always reducible in the ordinary sense since any linearised polynomial of degree > 1 has the nontrivial factor x. A linearised polynomial L(x) over F_q is symbolically irreducible if and only if its conventional q-associate l(x) is irreducible over F_q.

Every q-polynomial L(x) over F_q of degree > 1 has a symbolic factorization into symbolically irreducible polynomials over F_q and this factorization is essentially unique (up to rearranging factors and multiplying by nonzero elements of F_q.)

For example,^[6] consider the 2-polynomial L(x) = x¹⁶ + x⁸ + x² + x over F₂ and its conventional 2-associate l(x) = x⁴ + x³ + x + 1. The factorization into irreducibles of l(x) = (x² + x + 1)(x + 1)² in F₂[x], gives the symbolic factorization

L(x) = (x^4 + x^2 + x) \otimes (x^2 + x) \otimes (x^2 + x).

Affine polynomials

Let L be a linearised polynomial over 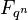$F_{q^n}$ . A polynomial of the form 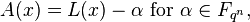$A(x) = L(x) - \alpha \text{ for } \alpha \in F_{q^n},$ is an affine polynomial over $F_{q^n}$ .

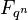Theorem: If A is a nonzero affine polynomial over 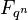$F_{q^n}$ with all of its roots lying in the field 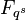$F_{q^s}$ an extension field of 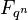$F_{q^n}$ , then each root of A has the same multiplicity, which is either 1, or a positive power of q.^[7]

Notes

↑ Lidl & Niederreiter 1983, pg.107 (first edition)
↑ Mullen & Panario 2013, p. 23 (2.1.106)
↑ Lidl & Niederreiter 1983, pg. 115 (first edition)
↑ Lidl & Niederreiter 1983, pg. 115 (first edition) Corollary 3.60
↑ Lidl & Neiderreiter 1983, pg. 116 (first edition) Theorem 3.62
↑ Lidl & Neiderreiter 1983, pg. 117 (first edition) Example 3.64
↑ Mullen & Panario 2013, p. 23 (2.1.109)

References

Lidl, Rudolf; Niederreiter, Harald (1997). Finite fields. Encyclopedia of Mathematics and Its Applications 20 (2nd ed.). Cambridge University Press. ISBN 0-521-39231-4. Zbl 0866.11069.
Mullen, Gary L.; Panario, Daniel (2013), Handbook of Finite Fields, Discrete Mathematics and its Applications, Boca Raton: CRC Press, ISBN 978-1-4398-7378-6

This article is issued from Wikipedia - version of the Sunday, July 19, 2015. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.