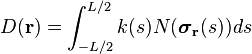Line integral convolution

LIC visualization of a flow field.

In scientific visualization, line integral convolution (LIC) is a technique proposed by Brian Cabral and Leith Leedom to visualize fluid motion, such as the wind movement in a tornado.^[1] Compared with simpler integration-like techniques, where one follows the flow vector at each point to produce a line, it has the advantage of producing a whole image at every step. It is a method from the texture advection family.

Principle

LIC visualization with color denoting velocity magnitude.

Intuition

Intuitively, the flow of a vector field is visualized by adding a random static pattern of dark and light paint sources. As the flow passes by the sources each parcel of fluid picks up some of the source color, averaging it with the color it has already acquired. Very similar to throwing paint in a river. The result is a random striped texture where points along the same streamline tend to have similar color.

Algorithm

Algorithmically, the technique generates a random gray level image at the desired output resolution. Then, for every pixel in the image, the forward and backward streamline of a fixed arc length is calculated. The convolution of a suitable convolution kernel with the gray levels of all the pixels that lie in this streamline is the value assigned to the current pixel in the output image.

Mathematic description

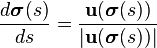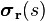Mathematically: let $\mathbf{u}$ be the vector field. Then a streamline parametrized by arc length can be defined as $\frac{d\boldsymbol \sigma (s)}{ds} = \frac{\mathbf{u}(\boldsymbol {\sigma}(s))}{|\mathbf{u}(\boldsymbol{\sigma}(s))|}$ . Let $\boldsymbol{\sigma}_\mathbf{r}(s)$ be the streamline that passes through the point $\mathbf{r}$ for $s=0$ . Then the image color at $\mathbf{r}$ can be set to

D(\mathbf{r}) = \int_{-L/2}^{L/2} k(s)N(\boldsymbol{\sigma}_{\mathbf{r}}(s)) ds

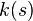where $k(s)$ is the convolution kernel, 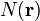$N(\mathbf{r})$ is the noise image, and $L$ the length of streamline that is followed. Note that there is no need to assume positions to be purely 2D: the method is applicable to surfaces in higher dimensions, using multidimensional noise fields.

The output image will normally be colored in some way. For the tornado example, the LIC output could determine the brightness of the color, while the vector length at each point would determine its hue. Different choices of convolution kernels and random noise can also produce different textures: for example pink noise produces a cloudy pattern where areas of higher flow stand out as smearing, suitable for weather visualisations. Further refinements in the convolution can improve the quality of the image.^[2]

Animated version

Illustration on how to animate. Above: Normal Box Filter (average). Middle: Sinusoidal Filter at

t

. Bottom: Sinusoidal Filter at

t + \delta t

LICs can be animated by using a kernel that changes over time. Samples at a constant time from the streamline would still be used, but instead of averaging all pixels in a streamline with a static kernel, a ripple-like kernel constructed from a periodic function multiplied by a Hann function acting as a window (in order to prevent artifacts) is used. The periodic function is then shifted along the period to create an animation.

Usability

In user testing the method was found to be particularly good for identifying critical points, but at least in the static case the method does not give an indication of the flow direction.^[3]

The main drawback of the method is the high computational demands. For each pixel 20-50 advected points have to be calculated, limiting interactivity. Performance can be improved by re-using parts of already computed streamlines. Various methods of graphics hardware acceleration have been attempted, mixing the pure convolution method with image-based flow visualization. ^[4]

References

↑ Cabral, Brian; Leedom, Leith Casey (August 2–6, 1993). "Imaging Vector Fields Using Line Integral Convolution". Proceedings of the 20th annual conference on Computer graphics and interactive techniques. SIGGRAPH '93. Anaheim, California. pp. 263–270. doi:10.1145/166117.166151. ISBN 0-89791-601-8. CiteSeerX: 10.1.1.115.1636.
↑ D. Weiskopf. Iterative twofold line integral convolution for texture-based vector field visualization. In T. Möller, B. Hamann, R. Russell (Eds.), Mathematical Foundations of Scientific Visualization, Computer Graphics, and Massive Data Exploration, Springer, 191-211, 2009. http://www.vis.uni-stuttgart.de/~weiskopf/publications/birs04.pdf
↑ Laidlaw, D.H., Kirby, R.M., Davidson, J.S., Miller, T.S., da Silva, M., Warren, W.H., Tarr, M. , Quantitative comparative evaluation of 2D vector field visualization methods, Visualization, 2001. VIS '01. Proceedings 21-26 Oct. 2001 pp. 143-150
↑ van Wijk, Jarke J. (2002), "Image based flow visualization", Proc. 29th Conf. Computer Graphics and Interactive Techniques (SIGGRAPH '02), pp. 745–754

External links

Tutorial including a lot of sample pictures

This article is issued from Wikipedia - version of the Thursday, October 15, 2015. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.