Lieb's square ice constant
| Binary | 1.10001010001000110100010111001100… |
| Decimal | 1.53960071783900203869106341467188… |
| Hexadecimal | 1.8A2345CC04425BC2CBF57DB94EDCA6B2… |
| Continued fraction |  |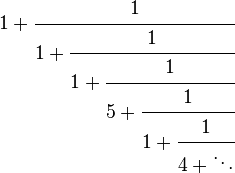
| Algebraic form |  |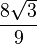
Lieb's square ice constant is a mathematical constant used in the field of combinatorics to quantify the number of Eulerian orientations of grid graphs. It was introduced by Elliott H. Lieb in 1967.[1]
Definition
An n × n grid graph (with periodic boundary conditions and n ≥ 2) has n2 vertices and 2n2 edges; it is 4-regular, meaning that each vertex has exactly four neighbors. An orientation of this graph is an assignment of a direction to each edge; it is an Eulerian orientation if it gives each vertex exactly two incoming edges and exactly two outgoing edges. Denote the number of Eulerian orientations of this graph by f(n). Then
![\lim_{n \to \infty}\sqrt[n^2]{f(n)}=\left(\frac{4}{3}\right)^\frac{3}{2}=\frac{8 \sqrt{3}}{9}=1.5396007\dots](../I/m/6de7c7221c91d4702db7236858e40f8f.png)
is Lieb's square ice constant.
Some historical and physical background can be found in the article Ice-type model.
See also
References
- ↑ Lieb, Elliott (1967). "Residual Entropy of Square Ice". Physical Review 162 (1): 162. doi:10.1103/PhysRev.162.162.
- ↑ (sequence A118273 in OEIS)
This article is issued from Wikipedia - version of the Sunday, January 18, 2015. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.