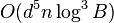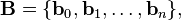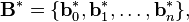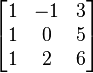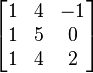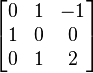Lenstra–Lenstra–Lovász lattice basis reduction algorithm
The Lenstra–Lenstra–Lovász (LLL) lattice basis reduction algorithm is a polynomial time lattice reduction algorithm invented by Arjen Lenstra, Hendrik Lenstra and László Lovász in 1982.[1] Given a basis 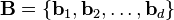 with n-dimensional integer coordinates, for a lattice L (a discrete subgroup of Rn) with
with n-dimensional integer coordinates, for a lattice L (a discrete subgroup of Rn) with 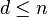 , the LLL algorithm calculates an LLL-reduced (short, nearly orthogonal) lattice basis in time
, the LLL algorithm calculates an LLL-reduced (short, nearly orthogonal) lattice basis in time
where B is the largest length of 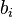 under the Euclidean norm.
under the Euclidean norm.
The original applications were to give polynomial-time algorithms for factorizing polynomials with rational coefficients, for finding simultaneous rational approximations to real numbers, and for solving the integer linear programming problem in fixed dimensions.
LLL reduction
The precise definition of LLL-reduced is as follows: Given a basis
define its Gram–Schmidt process orthogonal basis
and the Gram-Schmidt coefficients
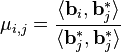 , for any
, for any 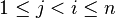 .
.
Then the basis  is LLL-reduced if there exists a parameter
is LLL-reduced if there exists a parameter 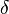 in (0.25,1] such that the following holds:
in (0.25,1] such that the following holds:
- (size-reduced) For
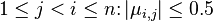 . By definition, this property guarantees the length reduction of the ordered basis.
. By definition, this property guarantees the length reduction of the ordered basis. - (Lovász condition) For k = 1,2,..,n
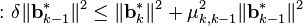 .
.
Here, estimating the value of the 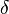 parameter, we can conclude how well the basis is reduced. Greater values of
parameter, we can conclude how well the basis is reduced. Greater values of 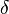 lead to stronger reductions of the basis.
Initially, A. Lenstra, H. Lenstra and L. Lovász demonstrated the LLL-reduction algorithm for
lead to stronger reductions of the basis.
Initially, A. Lenstra, H. Lenstra and L. Lovász demonstrated the LLL-reduction algorithm for 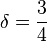 .
Note that although LLL-reduction is well-defined for
.
Note that although LLL-reduction is well-defined for 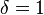 , the polynomial-time complexity is guaranteed only
for
, the polynomial-time complexity is guaranteed only
for 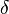 in (0.25,1).
in (0.25,1).
The LLL algorithm computes LLL-reduced bases. There is no known efficient algorithm to compute a basis in which the basis vectors are as short as possible for lattices of dimensions greater than 4. However, an LLL-reduced basis is nearly as short as possible, in the sense that there are absolute bounds 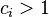 such that the first basis vector is no more than
such that the first basis vector is no more than 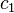 times as long as a shortest vector in the lattice,
the second basis vector is likewise within
times as long as a shortest vector in the lattice,
the second basis vector is likewise within 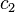 of the second successive minimum, and so on.
of the second successive minimum, and so on.
LLL Algorithm
The following description is based on (Hoffstein, Pipher & Silverman 2008, Theorem 6.68), with the corrections from the errata [2]
INPUT:
 a lattice basis
a lattice basis 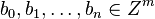 ,
, parameter
parameter 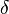 with
with 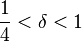 , most commonly
, most commonly 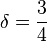
PROCEDURE:
Perform Gram-Schmidt, but do not normalize:Define
, which must always use the most current values of
. Let
while
do for j from
to 0 do if
do
Update ortho entries and related
's as needed. (The naive method is to recompute
whenever a
changes.) end if end for if
then
else Swap
and
. Update ortho entries and related
's as needed. (See above comment.)
end if end while
OUTPUT: LLL reduced basis 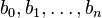
Example
The following presents an example due to W. Bosma.[3]
INPUT:
Let a lattice basis 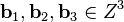 , be given by the columns of
, be given by the columns of
Then according to the LLL algorithm we obtain the following:
1.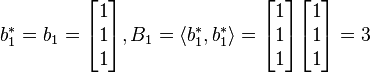
2.For  DO:
DO:
2.1.For 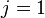 set
set 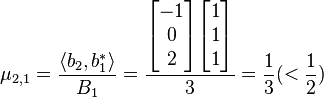
and 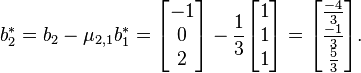
2.2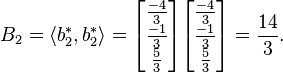
3. 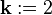
4.Here the step 4 of the LLL algorithm is skipped as size-reduced property holds for 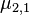
5.For 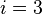 and for
and for 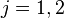 calculate
calculate 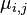 and
and 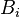 :
:
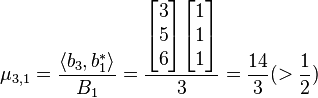
hence 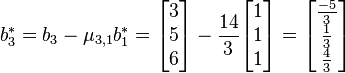
and 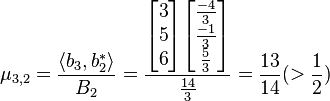
hence 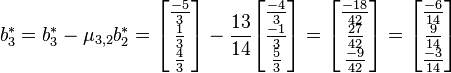 and
and

6.While 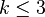 DO
DO
6.1 Length reduce 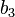 and correct
and correct 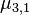 and
and 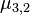 according to reduction subroutine in step 4:
according to reduction subroutine in step 4:
For 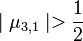 EXECUTE reduction subroutine RED(3,1):
EXECUTE reduction subroutine RED(3,1):
i.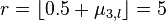 and
and 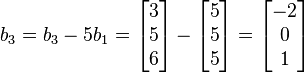
ii.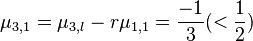
iii.Set 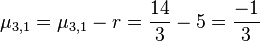
For 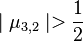 EXECUTE reduction subroutine RED(3,2):
EXECUTE reduction subroutine RED(3,2):
i.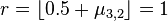 and
and 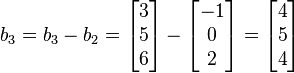
ii.Set 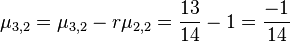
iii.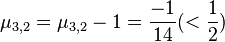
6.2 As 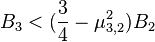 takes place, then
takes place, then
6.2.1 Exchange 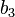 and
and 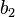
6.2.2  := 2
:= 2
Apply a SWAP, continue algorithm with the lattice basis, which is given by columns
Implement the algorithm steps again.
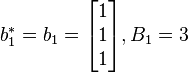
1.
2. 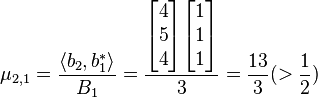
3. .
.
4.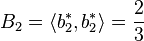 .
.
5.For 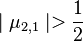 EXECUTE reduction subroutine RED(2,1):
EXECUTE reduction subroutine RED(2,1):
i.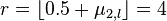 and
and 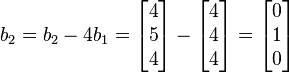
ii.Set 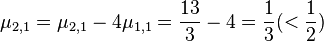
6. As 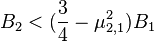 takes place, then
takes place, then
7. Exchange 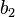 and
and 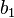
OUTPUT: LLL reduced basis
Applications
The LLL algorithm has found numerous other applications in MIMO detection algorithms [4] and cryptanalysis of public-key encryption schemes: knapsack cryptosystems, RSA with particular settings, NTRUEncrypt, and so forth. The algorithm can be used to find integer solutions to many problems.[5]
In particular, the LLL algorithm forms a core of one of the integer relation algorithms. For example, if it is believed that r=1.618034 is a (slightly rounded) root to an unknown quadratic equation with integer coefficients, one may apply LLL reduction to the lattice in 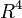 spanned by
spanned by ![[1,0,0,10000r^2], [0,1,0,10000r],](../I/m/3a09d44bae250cffef3372ccbf8ecfe0.png) and
and ![[0,0,1,10000]](../I/m/2594c427d5b4fb0cede2634481fcdd22.png) . The first vector in the reduced basis will be an integer linear combination of these three, thus necessarily of the form
. The first vector in the reduced basis will be an integer linear combination of these three, thus necessarily of the form ![[a,b,c,10000(ar^2+br+c)]](../I/m/c96def9c2898d637a08c9361591cff70.png) ; but such a vector is "short" only if a, b, c are small and
; but such a vector is "short" only if a, b, c are small and 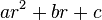 is even smaller. Thus the first three entries of this short vector are likely to be the coefficients of the integral quadratic polynomial which has r as a root. In this example the LLL algorithm finds the shortest vector to be [1, -1, -1, 0.00025] and indeed
is even smaller. Thus the first three entries of this short vector are likely to be the coefficients of the integral quadratic polynomial which has r as a root. In this example the LLL algorithm finds the shortest vector to be [1, -1, -1, 0.00025] and indeed 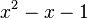 has a root equal to the golden ratio, 1.6180339887….
has a root equal to the golden ratio, 1.6180339887….
Implementations
LLL is implemented in
- Arageli as the function
lll_reduction_int - fpLLL as a stand-alone implementation
- GAP as the function
LLLReducedBasis - Macaulay2 as the function
LLLin the packageLLLBases - Magma as the functions
LLLandLLLGram(taking a gram matrix) - Maple as the function
IntegerRelations[LLL] - Mathematica as the function
LatticeReduce - Number Theory Library (NTL) as the function
LLL - PARI/GP as the function
qflll - Pymatgen as the function
analysis.get_lll_reduced_lattice - Sage as the method
LLLdriven by fpLLL and NTL
See also
Notes
- ↑ Lenstra, A. K.; Lenstra, H. W., Jr.; Lovász, L. (1982). "Factoring polynomials with rational coefficients". Mathematische Annalen 261 (4): 515–534. doi:10.1007/BF01457454. MR 0682664. hdl:1887/3810.
- ↑ Silverman, Joseph. "Introduction to Mathematical Cryptography Errata" (PDF). Brown University Mathematics Dept. Retrieved 5 May 2015.
- ↑ Bosma, Wieb. "4. LLL" (PDF). Lecture notes. Retrieved 28 February 2010.
- ↑ Shahabuddin, Shahriar et al., "A Customized Lattice Reduction Multiprocessor for MIMO Detection", in Arxiv preprint, January 2015.
- ↑ D. Simon (2007). "Selected applications of LLL in number theory" (PDF). LLL+25 Conference (Caen, France).
References
- Napias, Huguette (1996). "A generalizaion of the LLL algorithm over euclidean rings or orders". J. The. Nombr. Bordeaux 8 (2): 387–396.
- Cohen, Henri (2000). A course in computational algebraic number theory. GTM 138. Springer. ISBN 3-540-55640-0.
- Borwein, Peter (2002). Computational Excursions in Analysis and Number Theory. ISBN 0-387-95444-9.
- Luk, Franklin T.; Qiao, Sanzheng (2011). "A pivoted LLL algorithm". Lin. Alg. Appl. 434: 2296–2307. doi:10.1016/j.laa.2010.04.003.
- Hoffstein, Jeffrey; Pipher, Jill; Silverman, J.H. (2008). An Introduction to Mathematical Cryptography. Springer. ISBN 978-0-387-77993-5.