Lehmer's totient problem

In mathematics, Lehmer's totient problem, named for D. H. Lehmer, asks whether there is any composite number n such that Euler's totient function φ(n) divides n − 1. This is true of every prime number, and Lehmer conjectured in 1932 that there are no composite solutions: he showed that if any such n exists, it must be odd, square-free, and divisible by at least seven primes (i.e. ω(n) ≥ 7). Such a number must also be a Carmichael number.

Properties

• In 1980 Cohen and Hagis proved that n > 10²⁰ and that ω(n) ≥ 14.^[1]
• In 1988 Hagis showed that if 3 divides n then n > 10^1937042 and ω(n) ≥ 298848.^[2]
• The number of solutions to the problem less than X is 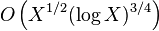.^[3]

References

• Cohen, Graeme L.; Hagis, Peter, jun. (1980). "On the number of prime factors of n if φ(n) divides n−1". Nieuw Arch. Wiskd., III. Ser. 28: 177–185. ISSN 0028-9825. Zbl 0436.10002. 
• Guy, Richard K. (2004). Unsolved problems in number theory (3rd ed.). Springer-Verlag. B37. ISBN 0-387-20860-7. Zbl 1058.11001. 
• Hagis, Peter, jun. (1988). "On the equation M⋅φ(n)=n−1". Nieuw Arch. Wiskd., IV. Ser. 6 (3): 255–261. ISSN 0028-9825. Zbl 0668.10006. 
• Lehmer, D. H. (1932). "On Euler's totient function". Bulletin of the American Mathematical Society 38: 745–751. doi:10.1090/s0002-9904-1932-05521-5. ISSN 0002-9904. Zbl 0005.34302. 
• Ribenboim, Paulo (1996). The New Book of Prime Number Records (3rd ed.). New York: Springer-Verlag. ISBN 0-387-94457-5. Zbl 0856.11001. 
• Sándor, József; Mitrinović, Dragoslav S.; Crstici, Borislav, eds. (2006). Handbook of number theory I. Dordrecht: Springer-Verlag. ISBN 1-4020-4215-9. Zbl 1151.11300. 

External links

• Weisstein, Eric W., "Lehmer's Totient Problem", MathWorld.