Legendre's conjecture

Legendre's conjecture, proposed by Adrien-Marie Legendre, states that there is a prime number between n2 and (n + 1)2 for every positive integer n. The conjecture is one of Landau's problems (1912) on prime numbers; as of 2015, the conjecture has neither been proved nor disproved.
Prime gaps
Legendre's conjecture is one of a family of results and conjectures related to prime gaps, that is, to the spacing between prime numbers.
The prime number theorem implies that the actual number of primes between n2 and (n + 1)2 ![]() A014085 is asymptotic to n/ln(n). Since this number is large for large n, this lends credence to Legendre's conjecture.
A014085 is asymptotic to n/ln(n). Since this number is large for large n, this lends credence to Legendre's conjecture.
If Legendre's conjecture is true, the gap between any prime p and the next largest prime would always be at most on the order of 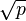 ;[a] in big O notation, the gaps are
;[a] in big O notation, the gaps are 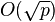 . Two stronger conjectures, Andrica's conjecture and Oppermann's conjecture, also both imply that the gaps have the same magnitude. It does not, however, provide a solution to the Riemann Hypothesis, but rather strengthens one of the implications of its correctness.
. Two stronger conjectures, Andrica's conjecture and Oppermann's conjecture, also both imply that the gaps have the same magnitude. It does not, however, provide a solution to the Riemann Hypothesis, but rather strengthens one of the implications of its correctness.
Harald Cramér conjectured that the gaps are always much smaller, of the order 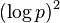 . If Cramér's conjecture is true, Legendre's conjecture would follow for all sufficiently large n. Cramér also proved that the Riemann hypothesis implies a weaker bound of
. If Cramér's conjecture is true, Legendre's conjecture would follow for all sufficiently large n. Cramér also proved that the Riemann hypothesis implies a weaker bound of 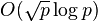 on the size of the largest prime gaps.[1]
on the size of the largest prime gaps.[1]
A counterexample near 1018 would require a prime gap fifty million times the size of the average gap.
Legendre's conjecture implies that at least one prime can be found in every half revolution of the Ulam spiral.
Partial results
Baker, Harman and Pintz proved that there is a prime in the interval ![[x,\,x+O(x^{21/40})]](../I/m/73af7ebbe5f19543878bfd4fd822eb32.png) for all large
for all large  .[2]
.[2]
A table of maximal prime gaps shows that the conjecture holds to 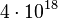 .[3]
.[3]
It has been proven that for infinitely many 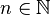 , we have
, we have
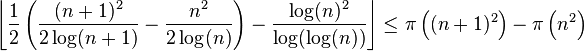 ,
,
where 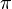 is the prime-counting function.[4]
is the prime-counting function.[4]
See also
Notes and references
- ^a This is a consequence of the fact that the difference between two consecutive squares is of the order of their square roots.
- ↑ Stewart, Ian (2013), Visions of Infinity: The Great Mathematical Problems, Basic Books, p. 164, ISBN 9780465022403.
- ↑ Baker, R. C.; Harman, G.; Pintz, G.; Pintz, J. (2001). "The difference between consecutive primes, II". Proceedings of the London Mathematical Society 83 (3): 532–562. doi:10.1112/plms/83.3.532.
- ↑ Oliveira e Silva, Tomás; Herzog, Siegfried; Pardi, Silvio (2014), "Empirical verification of the even Goldbach conjecture and computation of prime gaps up to
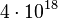 ", Mathematics of Computation 83 (288): 2033–2060, doi:10.1090/S0025-5718-2013-02787-1, MR 3194140.
", Mathematics of Computation 83 (288): 2033–2060, doi:10.1090/S0025-5718-2013-02787-1, MR 3194140. - ↑ Mehdi Hassani, Counting primes in the interval (n^2,(n+1)^2)