Lee-Kesler method

The Lee-Kesler method ^[1] allows the estimation of the saturated vapor pressure at a given temperature for all components for which the critical pressure P_c, the critical temperature T_c, and the acentric factor ω are known.

Equations

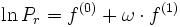
$\ln P_r = f^{(0)} + \omega \cdot f^{(1)}$

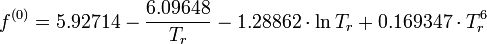
$f^{(0)}=5.92714 - \frac{6.09648}{T_r} - 1.28862 \cdot \ln T_r + 0.169347 \cdot T_r^6$

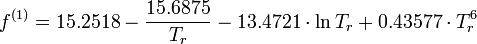
$f^{(1)}=15.2518 - \frac{15.6875}{T_r}-13.4721 \cdot \ln T_r + 0.43577 \cdot T_r^6$

with

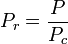$P_r=\frac{P}{P_c}$ (reduced pressure) and 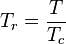$T_r=\frac{T}{T_c}$ (reduced temperature).

Typical errors

The prediction error can be up to 10% for polar components and small pressures and the calculated pressure is typically too low. For pressures above 1 bar, that means, above the normal boiling point, the typical errors are below 2%. ^[2]

Example calculation

For benzene with

T_c = 562.12 K^[3]
P_c = 4898 kPa^[3]
T_b = 353.15 K^[4]
ω = 0.2120^[5]

the following calculation for T=T_b results:

T_r = 353.15 / 562.12 = 0.628247
f⁽⁰⁾ = -3.167428
f⁽¹⁾ = -3.429560
P_r = exp( f⁽⁰⁾ + ω f⁽¹⁾ ) = 0.020354
P = P_r * P_c = 99.69 kPa

The correct result would be P = 101.325 kPa, the normal (atmospheric) pressure. The deviation is -1.63 kPa or -1.61 %.

It is important to use the same absolute units for T and T_c as well as for P and P_c. The unit system used (K or R for T) is irrelevant because of the usage of the reduced values T_r and P_r.

References

↑ Lee B.I., Kesler M.G., "A Generalized Thermodynamic Correlation Based on Three-Parameter Corresponding States", AIChE J., 21(3), 510-527, 1975
↑ Reid R.C., Prausnitz J.M., Poling B.E., "The Properties of Gases & Liquids", 4. Auflage, McGraw-Hill, 1988
1 2 Brunner E., Thies M.C., Schneider G.M., J.Supercrit.Fluids, 39(2), 160-173, 2006
↑ Silva L.M.C., Mattedi S., Gonzalez-Olmos R., Iglesias M., J.Chem.Thermodyn., 38(12), 1725-1736, 2006
↑ Dortmund Data Bank

This article is issued from Wikipedia - version of the Sunday, March 02, 2014. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.