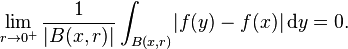Lebesgue point

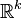In mathematics, given a locally Lebesgue integrable function $f$ on $\mathbb{R}^k$ , a point $x$ in the domain of $f$ is a Lebesgue point if^[1]

\lim_{r\rightarrow 0^+}\frac{1}{|B(x,r)|}\int_{B(x,r)} \!|f(y)-f(x)|\,\mathrm{d}y=0.

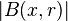Here, $B(x,r)$ is a ball centered at $x$ with radius $r > 0$ , and $|B(x,r)|$ is its Lebesgue measure. The Lebesgue points of $f$ are thus points where $f$ does not oscillate too much, in an average sense.^[2]

The Lebesgue differentiation theorem states that, given any 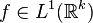$f\in L^1(\mathbb{R}^k)$ , almost every $x$ is a Lebesgue point.^[3]

References

↑ Bogachev, Vladimir I. (2007), Measure Theory, Volume 1, Springer, p. 351, ISBN 9783540345145 .
↑ Martio, Olli; Ryazanov, Vladimir; Srebro, Uri; Yakubov, Eduard (2008), Moduli in Modern Mapping Theory, Springer Monographs in Mathematics, Springer, p. 105, ISBN 9780387855882 .
↑ Giaquinta, Mariano; Modica, Giuseppe (2010), Mathematical Analysis: An Introduction to Functions of Several Variables, Springer, p. 80, ISBN 9780817646127 .

This article is issued from Wikipedia - version of the Wednesday, May 20, 2015. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.