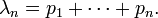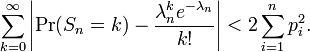Le Cam's theorem

In probability theory, Le Cam's theorem, named after Lucien le Cam (1924 – 2000), states the following. ^[1]^[2]^[3]

Suppose:

X₁, ..., X_n are independent random variables, each with a Bernoulli distribution (i.e., equal to either 0 or 1), not necessarily identically distributed.

Pr(X_i = 1) = p_i for i = 1, 2, 3, ...

$\lambda_n = p_1 + \cdots + p_n.\,$

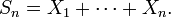$S_n = X_1 + \cdots + X_n.\,$ (i.e. $S_n$ follows a Poisson binomial distribution)

Then

\sum_{k=0}^\infty \left| \Pr(S_n=k) - {\lambda_n^k e^{-\lambda_n} \over k!} \right| < 2 \sum_{i=1}^n p_i^2.

In other words, the sum has approximately a Poisson distribution and the above inequality bounds the approximation error in terms of the total variation distance.

By setting p_i = λ_n/n, we see that this generalizes the usual Poisson limit theorem.

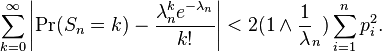When $\lambda_n$ is a large a better bound is possible: : $\sum_{k=0}^\infty \left| \Pr(S_n=k) - {\lambda_n^k e^{-\lambda_n} \over k!} \right| < 2 (1 \wedge \frac 1 \lambda_n) \sum_{i=1}^n p_i^2.$ It is also possible to weaken the independence requirement.^[4]

References

↑ Le Cam, L. (1960). "An Approximation Theorem for the Poisson Binomial Distribution". Pacific Journal of Mathematics 10 (4): 1181–1197. doi:10.2140/pjm.1960.10.1181. MR 0142174. Zbl 0118.33601. Retrieved 2009-05-13.
↑ Le Cam, L. (1963). "On the Distribution of Sums of Independent Random Variables". In Jerzy Neyman; Lucien le Cam. Bernoulli, Bayes, Laplace: Proceedings of an International Research Seminar. New York: Springer-Verlag. pp. 179–202. MR 0199871.
↑ Steele, J. M. (1994). "Le Cam's Inequality and Poisson Approximations". The American Mathematical Monthly 101 (1): 48–54. doi:10.2307/2325124. JSTOR 2325124.
↑ den Hollander, Frank. Probability Theory: the Coupling Method.

External links

Weisstein, Eric W., "Le Cam's Inequality", MathWorld.

This article is issued from Wikipedia - version of the Tuesday, February 09, 2016. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.