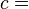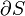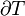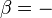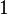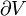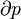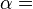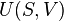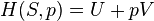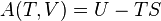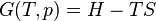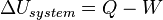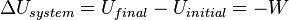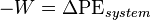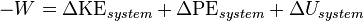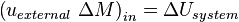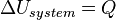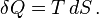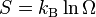Laws of thermodynamics
| Thermodynamics | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
The classical Carnot heat engine | ||||||||||||
|
Branches |
||||||||||||
|
||||||||||||
| Book:Thermodynamics | ||||||||||||
The four laws of thermodynamics define fundamental physical quantities (temperature, energy, and entropy) that characterize thermodynamic systems. The laws describe how these quantities behave under various circumstances, and forbid certain phenomena (such as perpetual motion).
The four laws of thermodynamics are:[1][2][3][4][5]
- Zeroth law of thermodynamics: If two systems are in thermal equilibrium independently with a third system, they must be in thermal equilibrium with each other. This law helps define the notion of temperature.
- First law of thermodynamics: When energy passes, as work, as heat, or with matter, into or out from a system, its internal energy changes in accord with the law of conservation of energy. Equivalently, perpetual motion machines of the first kind are impossible.
- Second law of thermodynamics: In a natural thermodynamic process, the sum of the entropies of the interacting thermodynamic systems increases. Equivalently, perpetual motion machines of the second kind are impossible.
- Third law of thermodynamics: The entropy of a system approaches a constant value as the temperature approaches absolute zero.[2] With the exception of non-crystalline solids (glasses) the entropy of a system at absolute zero is typically close to zero, and is equal to the logarithm of the multiplicity of the quantum ground states.
There have been suggestions of additional laws, but none of them achieves the generality of the four accepted laws, and they are not mentioned in standard textbooks.[1][2][3][4][6][7]
The laws of thermodynamics are important fundamental laws in physics and they are applicable in other natural sciences.
Zeroth law
The zeroth law of thermodynamics may be stated in the following form:
If two systems are both in thermal equilibrium with a third system then they are in thermal equilibrium with each other.[8]
The law is intended to allow the existence of an empirical parameter, the temperature, as a property of a system such that systems in thermal equilibrium with each other have the same temperature. The law as stated here is compatible with the use of a particular physical body, for example a mass of gas, to match temperatures of other bodies, but does not justify regarding temperature as a quantity that can be measured on a scale of real numbers.
Though this version of the law is one of the more commonly stated, it is only one of a diversity of statements that are labeled as "the zeroth law" by competent writers. Some statements go further so as to supply the important physical fact that temperature is one-dimensional, that one can conceptually arrange bodies in real number sequence from colder to hotter.[9][10][11] Perhaps there exists no unique "best possible statement" of the "zeroth law", because there is in the literature a range of formulations of the principles of thermodynamics, each of which call for their respectively appropriate versions of the law.
Although these concepts of temperature and of thermal equilibrium are fundamental to thermodynamics and were clearly stated in the nineteenth century, the desire to explicitly number the above law was not widely felt until Fowler and Guggenheim did so in the 1930s, long after the first, second, and third law were already widely understood and recognized. Hence it was numbered the zeroth law. The importance of the law as a foundation to the earlier laws is that it allows the definition of temperature in a non-circular way without reference to entropy, its conjugate variable. Such a temperature definition is said to be 'empirical'.[12][13][14][15][16][17]
First law
The first law of thermodynamics may be stated in several ways :
- The increase in internal energy of a closed system is equal to the heat supplied to the system minus work done by it.
- For a thermodynamic cycle of a closed system, which returns to its original state, the heat Qin supplied to a closed system in one stage of the cycle, minus that Qout removed from it in another stage of the cycle, equals the net work done by the system.
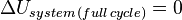 , and, consequently
, and, consequently 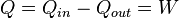
- The increase in internal energy of an adiabatically isolated system can only be the result of the net work performed by the system, because Q = 0.
More specifically, the First Law encompasses several principles:
- This states that energy can be neither created nor destroyed. However, energy can change forms, and energy can flow from one place to another. The total energy of an isolated system does not change.
- The concept of internal energy and its relationship to temperature.
- If a system has a definite temperature, then its total energy has three distinguishable components. If the system is in motion as a whole, it has kinetic energy. If the system as a whole is in an externally imposed force field (e.g. gravity), it has potential energy relative to some reference point in space. Finally, it has internal energy, which is a fundamental quantity for thermodynamics. The establishment of the concept of internal energy is the characteristic distinguishing feature of the first law of thermodynamics.
- Beyond the conceptual frame of macroscopic thermodynamics, internal energy can be explained as the sum of the diverse kinetic energies of the erratic microscopic motions of its constituent atoms, and of the potential energy of interactions between them. Other things being equal, the total of the kinetic energies of microscopic motions of the constituent atoms increases as the system's temperature increases.
- Work is a process of transferring energy to or from a system in ways that can be described by macroscopic mechanical forces exerted by factors in the surroundings, outside the system. Examples are an externally driven shaft agitating a stirrer within the system, or an externally imposed electric field that polarizes the material of the system, or a piston that compresses it. Unless otherwise stated, it is customary to treat work as occurring without dissipation in the surroundings. Within the system, in a natural process, some of the transferred work is dissipated by internal friction or viscosity. The work done by the system can come from its overall kinetic energy, from its overall potential energy, or from its internal energy.
- For example, when an externally driven machine lifts a system upwards, some energy is transferred from the machine to the system. The system acquires its energy in the form of gravitational potential energy in this example.
- Or in general it can be partitioned to kinetic, potential or internal energy
- When matter is transferred, its associated internal energy and overall potential energy are transferred with it.
- where uexternal denotes the internal energy per unit mass of the transferred matter, measured when it is still in the surroundings, before transfer; and ΔM denotes the transferred mass.
- The flow of heat is a form of energy transfer.
- Heating is a natural process of moving energy to or from a system other than by work or the transfer of matter. Direct passage of heat is only from a hotter to a colder system.
- If the system has rigid walls impermeable to matter, and no external long-range force field affects it, and consequently energy cannot be transferred as work into or out from the system, then:
where Q denotes the amount of energy transferred into the system as heat.
Combining these principles leads to one traditional statement of the first law of thermodynamics: it is not possible to construct a machine which will perpetually output work without an equal amount of energy input to that machine. Or more briefly, a perpetual motion machine of the first kind is impossible.
Second law
The second law of thermodynamics indicates the irreversibility of natural processes, and, in many cases, the tendency of natural processes to lead towards spatial homogeneity of matter and energy, and especially of temperature. It can be formulated in a variety of interesting and important ways.
It implies the existence of a quantity called the entropy of a thermodynamic system. In terms of this quantity it implies that
When two initially isolated systems in separate but nearby regions of space, each in thermodynamic equilibrium with itself but not necessarily with each other, are then allowed to interact, they will eventually reach a mutual thermodynamic equilibrium. The sum of the entropies of the initially isolated systems is less than or equal to the total entropy of the final combination. Equality occurs just when the two original systems have all their respective intensive variables (temperature, pressure) equal; then the final system also has the same values.
This statement of the law recognizes that in classical thermodynamics, the entropy of a system is defined only when it has reached its own internal thermodynamic equilibrium.
The second law refers to a wide variety of processes, reversible and irreversible. All natural processes are irreversible. Reversible processes are a convenient theoretical fiction and do not occur in nature.
A prime example of irreversibility is in the transfer of heat by conduction or radiation. It was known long before the discovery of the notion of entropy that when two bodies initially of different temperatures come into thermal connection, then heat always flows from the hotter body to the colder one.
The second law tells also about kinds of irreversibility other than heat transfer, for example those of friction and viscosity, and those of chemical reactions. The notion of entropy is needed to provide that wider scope of the law.
According to the second law of thermodynamics, in a theoretical and fictive reversible heat transfer, an element of heat transferred, δQ, is the product of the temperature (T), both of the system and of the sources or destination of the heat, with the increment (dS) of the system's conjugate variable, its entropy (S)
Entropy may also be viewed as a physical measure of the lack of physical information about the microscopic details of the motion and configuration of a system, when only the macroscopic states are known. The law asserts that for two given macroscopically specified states of a system, there is a quantity called the difference of information entropy between them. This information entropy difference defines how much additional microscopic physical information is needed to specify one of the macroscopically specified states, given the macroscopic specification of the other - often a conveniently chosen reference state which may be presupposed to exist rather than explicitly stated. A final condition of a natural process always contains microscopically specifiable effects which are not fully and exactly predictable from the macroscopic specification of the initial condition of the process. This is why entropy increases in natural processes - the increase tells how much extra microscopic information is needed to distinguish the final macroscopically specified state from the initial macroscopically specified state.[18]
Third law
The third law of thermodynamics is sometimes stated as follows:
- The entropy of a perfect crystal of any pure substance approaches zero as the temperature approaches absolute zero.
At zero temperature the system must be in a state with the minimum thermal energy. This statement holds true if the perfect crystal has only one state with minimum energy. Entropy is related to the number of possible microstates according to:
Where S is the entropy of the system, kB Boltzmann's constant, and Ω the number of microstates (e.g. possible configurations of atoms). At absolute zero there is only 1 microstate possible (Ω=1 as all the atoms are identical for a pure substance and as a result all orders are identical as there is only one combination) and ln(1) = 0.
A more general form of the third law that applies to a system such as a glass that may have more than one minimum microscopically distinct energy state, or may have a microscopically distinct state that is "frozen in" though not a strictly minimum energy state and not strictly speaking a state of thermodynamic equilibrium, at absolute zero temperature:
- The entropy of a system approaches a constant value as the temperature approaches zero.
The constant value (not necessarily zero) is called the residual entropy of the system.
History
Circa 1797, Count Rumford (born Benjamin Thompson) showed that endless mechanical action can generate indefinitely large amounts of heat from a fixed amount of working substance thus challenging the caloric theory of the time, which held that there would be a finite amount of caloric heat/energy in a fixed amount of working substance. The first established thermodynamic principle, which eventually became the second law of thermodynamics, was formulated by Sadi Carnot in 1824. By 1860, as formalized in the works of those such as Rudolf Clausius and William Thomson, two established principles of thermodynamics had evolved, the first principle and the second principle, later restated as thermodynamic laws. By 1873, for example, thermodynamicist Josiah Willard Gibbs, in his memoir Graphical Methods in the Thermodynamics of Fluids, clearly stated the first two absolute laws of thermodynamics. Some textbooks throughout the 20th century have numbered the laws differently. In some fields removed from chemistry, the second law was considered to deal with the efficiency of heat engines only, whereas what was called the third law dealt with entropy increases. Directly defining zero points for entropy calculations was not considered to be a law. Gradually, this separation was combined into the second law and the modern third law was widely adopted.
See also
- Conservation law
- Entropy production
- Ginsberg's theorem
- Heat death of the universe
- Laws of science
- Onsager reciprocal relations (sometimes described as a fourth law of thermodynamics)
- Table of thermodynamic equations
References
- 1 2 3 Guggenheim, E.A. (1985). Thermodynamics. An Advanced Treatment for Chemists and Physicists, seventh edition, North Holland, Amsterdam, ISBN 0-444-86951-4.
- 1 2 3 Kittel, C. Kroemer, H. (1980). Thermal Physics, second edition, W.H. Freeman, San Francisco, ISBN 0-7167-1088-9.
- 1 2 Adkins, C.J. (1968). Equilibrium Thermodynamics, McGraw-Hill, London, ISBN 0-07-084057-1.
- 1 2 Lebon, G., Jou, D., Casas-Vázquez, J. (2008). Understanding Non-equilibrium Thermodynamics. Foundations, Applications, Frontiers, Springer, Berlin, ISBN 978-3-540-74252-4.
- ↑ Chris Vuille; Serway, Raymond A.; Faughn, Jerry S. (2009). College physics. Belmont, CA: Brooks/Cole, Cengage Learning. p. 355. ISBN 0-495-38693-6.
- ↑ De Groot, S.R., Mazur, P. (1962). Non-equilibrium Thermodynamics, North Holland, Amsterdam.
- ↑ Glansdorff, P., Prigogine, I. (1971). Thermodynamic Theory of Structure, Stability and Fluctuations, Wiley-Interscience, London, ISBN 0-471-30280-5.
- ↑ Guggenheim (1985), p. 8.
- ↑ Sommerfeld, A. (1951/1955). Thermodynamics and Statistical Mechanics, vol. 5 of Lectures on Theoretical Physics, edited by F. Bopp, J. Meixner, translated by J. Kestin, Academic Press, New York, page 1.
- ↑ Serrin, J. (1978). The concepts of thermodynamics, in Contemporary Developments in Continuum Mechanics and Partial Differential Equations. Proceedings of the International Symposium on Continuum Mechanics and Partial Differential Equations, Rio de Janeiro, August 1977, edited by G.M. de La Penha, L.A.J. Medeiros, North-Holland, Amsterdam, ISBN 0-444-85166-6, pages 411-451.
- ↑ Serrin, J. (1986). Chapter 1, 'An Outline of Thermodynamical Structure', pages 3-32, in New Perspectives in Thermodynamics, edited by J. Serrin, Springer, Berlin, ISBN 3-540-15931-2.
- ↑ Adkins, C.J. (1968/1983). Equilibrium Thermodynamics, (first edition 1968), third edition 1983, Cambridge University Press, ISBN 0-521-25445-0, pp. 18–20.
- ↑ Bailyn, M. (1994). A Survey of Thermodynamics, American Institute of Physics Press, New York, ISBN 0-88318-797-3, p. 26.
- ↑ Buchdahl, H.A. (1966), The Concepts of Classical Thermodynamics, Cambridge University Press, London, pp. 30, 34ff, 46f, 83.
- ↑
- Münster, A. (1970), Classical Thermodynamics, translated by E.S. Halberstadt, Wiley–Interscience, London, ISBN 0-471-62430-6, p. 22.
- ↑ Pippard, A.B. (1957/1966). Elements of Classical Thermodynamics for Advanced Students of Physics, original publication 1957, reprint 1966, Cambridge University Press, Cambridge UK, p. 10.
- ↑ Wilson, H.A. (1966). Thermodynamics and Statistical Mechanics, Cambridge University Press, London UK, pp. 4, 8, 68, 86, 97, 311.
- ↑ Ben-Naim, A. (2008). A Farewell to Entropy: Statistical Thermodynamics Based on Information, World Scientific, New Jersey, ISBN 978-981-270-706-2.
Further reading
- Atkins, Peter, 2007. Four Laws That Drive the Universe. OUP Oxford.
- Goldstein, Martin, and Inge F., 1993. The Refrigerator and the Universe. Harvard Univ. Press. A gentle introduction.
External Links
- In Our Time: Perpetual Motion, BBC discussion about the Laws, with Ruth Gregory, Frank Close and Steven Bramwell, hosted by Melvyn Bragg, first broadcast 24 September 2015.