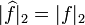Large sieve

In mathematics, the large sieve is a method (or family of methods and related ideas) in analytic number theory.

Its name comes from its original application: given a set 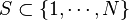$S\subset \{1,\cdots,N\}$ such that the elements of S are forbidden to lie in a set A_p ⊂ Z/p Z modulo every prime p, how large can S be? Here A_p is thought of as being large, i.e., at least as large as a constant times p; if this is not the case, we speak of a small sieve. (The term "sieve" is seen as alluding to, say, sifting ore for gold: we "sift out" the integers falling in one of the forbidden congruence classes modulo p, and ask ourselves how much is left at the end.)

Development

Large-sieve methods have been developed enough that they are applicable to small-sieve situations as well. By now, something is seen as related to the large sieve not necessarily in terms of whether it related to the kind situation outlined above, but, rather, if it involves one of the two methods of proof traditionally used to yield a large-sieve result:

Approximate Plancherel inequality

If a set 'S' is ill-distributed modulo p (by virtue, for example, of being excluded from the congruence classes A_p) then the Fourier coefficients 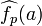$\widehat{f_p}(a)$ of the characteristic function f_p of the set S mod p are in average large. These coefficients can be lifted to values 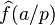$\widehat{f}(a/p)$ of the Fourier transform 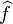$\widehat{f}$ of the characteristic function f of the set S (i.e.,

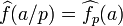\widehat{f}(a/p)=\widehat{f_p}(a)

By bounding derivatives, we can see that 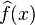$\widehat{f}(x)$ must be large, on average, for all x near rational numbers of the form a/p. Large here means "a relatively large constant times |S|". Since

|f|_2 = \sqrt{|S|}

we get a contradiction with the Plancherel identity

|\widehat{f}|_2=|f|_2

unless |S| is small. (In practice, to optimise bounds, people nowadays modify the Plancherel identity into an equality rather than bound derivatives as above.)

Duality principle

One can prove a strong large-sieve result easily by noting the following basic fact from functional analysis: the norm of a linear operator (i.e.,

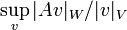\sup_v |Av|_W/|v|_V

where A is an operator from a linear space V to a linear space W) equals the norm of its adjoint i.e.,

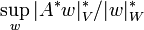\sup_w |A^* w|^*_V/|w|^*_W

This principle itself has come to acquire the name "large sieve" in some of the mathematical literature.

It is also possible to derive the large sieve from majorants in the style of Selberg (see Selberg, Collected Works, vol II, Lectures on sieves).

History

The early history of the large sieve traces back to work of Yu. B. Linnik, in 1941, working on the problem of the least quadratic non-residue. Subsequently Alfréd Rényi worked on it, using probability methods. It was only two decades later, after quite a number of contributions by others, that the large sieve was formulated in a way that was more definitive. This happened in the early 1960s, in independent work of Klaus Roth and Enrico Bombieri. It is also around that time that the connection with the duality principle became better understood.

References

Hazewinkel, Michiel, ed. (2001), "l/l057580", Encyclopedia of Mathematics, Springer, ISBN 978-1-55608-010-4
Cojocaru, Alina Carmen; Murty, M. Ram. An introduction to sieve methods and their applications. London Mathematical Society Student Texts 66. Cambridge University Press. pp. 135–155. ISBN 0-521-61275-6. Zbl 1121.11063.
Davenport, Harold (2000). Multiplicative Number Theory. Graduate Texts in Mathematics 74. Revised and with a preface by Hugh L. Montgomery (3rd ed.). Springer-Verlag. ISBN 0-387-95097-4. Zbl 1002.11001.
Friedlander, John; Iwaniec, Henryk (2010). Opera de Cribro. AMS Colloquium Publications. ISBN 978-0-8218-4970-5. Zbl 1226.11099.
Hooley, Christopher (1976). Applications of sieve methods to the theory of numbers. Cambridge University Press. pp. 17–20. ISBN 0-521-20915-3.
Kowalski, Emmanuel (2008). The Large Sieve and its Applications. Cambridge Tracts in Mathematics. Cambridge University Press. ISBN 978-0-521-88851-6.
Tenenbaum, Gérald (1995). Introduction to Analytic and Probabilistic Number Theory. Cambridge studies in advanced mathematics 46. Cambridge University Press. pp. 62–73. ISBN 0-521-41261-7.

This article is issued from Wikipedia - version of the Saturday, December 13, 2014. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.