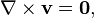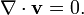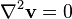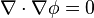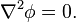Laplacian vector field

In vector calculus, a Laplacian vector field is a vector field which is both irrotational and incompressible. If the field is denoted as v, then it is described by the following differential equations:

\nabla \times \mathbf{v} = \mathbf{0},

\nabla \cdot \mathbf{v} = 0.

From the vector calculus identity 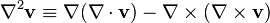$\nabla^2 \mathbf{v} \equiv \nabla (\nabla\cdot \mathbf{v}) - \nabla\times (\nabla\times \mathbf{v})$ it follows that

\nabla^2 \mathbf{v} = 0

that is, that the field v satisfies Laplace's equation.

A Laplacian vector field in the plane satisfies the Cauchy–Riemann equations: it is holomorphic.

Since the curl of v is zero, it follows that v can be expressed as the gradient of a scalar potential (see irrotational field) φ :

\mathbf{v} = \nabla \phi. \qquad \qquad (1)

Then, since the divergence of v is also zero, it follows from equation (1) that

\nabla \cdot \nabla \phi = 0

which is equivalent to

\nabla^2 \phi = 0.

Therefore, the potential of a Laplacian field satisfies Laplace's equation.

See also

This article is issued from Wikipedia - version of the Wednesday, February 10, 2016. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.