Langlands decomposition
In mathematics, the Langlands decomposition writes a parabolic subgroup P of a semisimple Lie group as a product 
of a reductive subgroup M, an abelian subgroup A, and a nilpotent subgroup N.
Applications
See also: Parabolic induction
A key application is in parabolic induction, which leads to the Langlands program: if 
is a reductive algebraic group and is the Langlands decomposition of a parabolic subgroup P, then parabolic induction consists of taking a representation of 
, extending it to 
by letting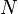 
act trivially, and inducing the result from to .
See also
References
- A. W. Knapp, Structure theory of semisimple Lie groups. ISBN 0-8218-0609-2.
This article is issued from Wikipedia - version of the Sunday, November 09, 2014. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.