Lamport timestamps
The algorithm of Lamport timestamps is a simple algorithm used to determine the order of events in a distributed computer system. As different nodes or processes will typically not be perfectly synchronized, this algorithm is used to provide a partial ordering of events with minimal overhead, and conceptually provide a starting point for the more advanced vector clock method. They are named after their creator, Leslie Lamport.
Distributed algorithms such as resource synchronization often depend on some method of ordering events to function. For example, consider a system with two processes and a disk. The processes send messages to each other, and also send messages to the disk requesting access. The disk grants access in the order the messages were sent. For example process A sends a message to the disk requesting write access, and then sends a read instruction message to process B. Process B receives the message, and as a result sends its own read request message to the disk. If there is a timing delay causing the disk to receive both messages at the same time, it can determine which message happened-before the other: ( happens-before
happens-before  if one can get from
if one can get from  to
to  by a sequence of moves of two types: moving forward while remaining in the same process, and following a message from its sending to its reception.) A logical clock algorithm provides a mechanism to determine facts about the order of such events.
by a sequence of moves of two types: moving forward while remaining in the same process, and following a message from its sending to its reception.) A logical clock algorithm provides a mechanism to determine facts about the order of such events.
Lamport invented a simple mechanism by which the happened-before ordering can be captured numerically. A Lamport logical clock is an incrementing software counter maintained in each process.
Conceptually, this logical clock can be thought of as a clock that only has meaning in relation to messages moving between processes. When a process receives a message, it resynchronizes its logical clock with that sender.
Algorithm
The algorithm follows some simple rules:
- A process increments its counter before each event in that process;
- When a process sends a message, it includes its counter value with the message;
- On receiving a message, the receiver sets its counter greater than or equal to its own counter (already incremented due to rule 1) and greater than the message counter, before it considers the message received.[1]
In a Pseudocode format, the algorithm for sending:
time = time+1; time_stamp = time; send(Message, time_stamp);
The algorithm for receiving a message:
(message, time_stamp) = receive(); time = max(time_stamp, time)+1;
Considerations
For every two different events  and
and  occurring in the same process, and
occurring in the same process, and  being the timestamp for a certain event
being the timestamp for a certain event  , it is necessary that
, it is necessary that  never equals
never equals 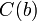 .
.
Therefore it is necessary that:
- The logical clock be set so that there is minimum of one clock "tick" (increment of the counter) between events
 and
and  ;
; - In a multiprocess or multithreaded environment, it might be necessary to attach the process ID (PID) or any other unique ID to the timestamp so that it is possible to differentiate between events
 and
and  which may occur simultaneously in different processes.
which may occur simultaneously in different processes.
Implications
A Lamport clock may be used to create a partial causal ordering of events between processes. Given a logical clock following these rules, the following relation is true: if 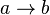 then
then 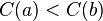 , where
, where 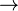 means happened-before.
means happened-before.
This relation only goes one way, and is called clock consistency condition: if one event comes before another, then that event's logical clock comes before the other's. The strong clock consistency condition, which is two way (if 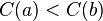 then
then 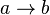 ), can be obtained by other techniques such as vector clocks. Using only a simple Lamport clock, only a partial causal ordering can be inferred from the clock.
), can be obtained by other techniques such as vector clocks. Using only a simple Lamport clock, only a partial causal ordering can be inferred from the clock.
However, via the contrapositive, it's true that  implies
implies  . So, for example, if
. So, for example, if  then
then  cannot have happened-before
cannot have happened-before  .
.
Another way of putting this is that 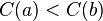 means that
means that  may have happened-before
may have happened-before  , or be incomparable with
, or be incomparable with  in the happened-before ordering, but
in the happened-before ordering, but  did not happen after
did not happen after  .
.
Nevertheless, Lamport timestamps can be used to create a total ordering of events in a distributed system by using some arbitrary mechanism to break ties (e.g. the ID of the process). The caveat is that this ordering is artifactual and cannot be depended on to imply a causal relationship.
Lamport's logical clock in distributed systems
- In a distributed system, it is not possible in practice to synchronize time across entities (typically thought of as processes) within the system; hence, the entities can use the concept of a logical clock based on the events through which they communicate.
- If two entities do not exchange any messages, then they probably do not need to share a common clock; events occurring on those entities are termed as concurrent events.
- Among the processes on the same local machine we can order the events based on the local clock of the system.
- When two entities communicate by message passing, then the send event is said to 'happen before' the receive event, and the logical order can be established among the events.
- A distributed system is said to have partial order if we can have a partial order relationship among the events in the system. If 'totality', i.e., causal relationship among all events in the system, can be established, then the system is said to have total order.
- A single entity cannot have two events occur simultaneously. If the system has total order we can determine the order among all events in the system. If the system has partial order between processes, which is the type of order Lamport's logical clock provides, then we can only tell the ordering between entities that interact. Lamport addressed ordering two events with the same timestamp (or counter): "To break ties, we use any arbitrary total ordering < of the processes."[2] Thus two timestamps or counters may be the same within a distributed system, but in applying the logical clocks algorithm events that occur will always maintain at least a strict partial ordering.
See also
References
- ↑ Lamport, L. (1978). "Time, clocks, and the ordering of events in a distributed system" (PDF). Communications of the ACM 21 (7): 560. doi:10.1145/359545.359563.
- ↑ Lamport, L. (1978). "Time, clocks, and the ordering of events in a distributed system" (PDF). Communications of the ACM 21 (7): 558–565. doi:10.1145/359545.359563.