Lagrange bracket
Lagrange brackets are certain expressions closely related to Poisson brackets that were introduced by Joseph Louis Lagrange in 1808–1810 for the purposes of mathematical formulation of classical mechanics, but unlike the Poisson brackets, have fallen out of use.
Definition
Suppose that (q1, …, qn, p1, …, pn) is a system of canonical coordinates on a phase space. If each of them is expressed as a function of two variables, u and v, then the Lagrange bracket of u and v is defined by the formula
Properties
- Lagrange brackets do not depend on the system of canonical coordinates (q, p). If (Q,P) = (Q1, …, Qn, P1, …, Pn) is another system of canonical coordinates, so that
- is a canonical transformation, then the Lagrange bracket is an invariant of the transformation, in the sense that
- Therefore, the subscripts indicating the canonical coordinates are often omitted.
- If Ω is the symplectic form on the 2n-dimensional phase space W and u1,…,u2n form a system of coordinates on W, then canonical coordinates (q,p) may be expressed as functions of the coordinates u and the matrix of the Lagrange brackets
- represents the components of Ω, viewed as a tensor, in the coordinates u. This matrix is the inverse of the matrix formed by the Poisson brackets
- of the coordinates u.
- As a corollary of the preceding properties, coordinates (Q1, …, Qn, P1, …, Pn) on a phase space are canonical if and only if the Lagrange brackets between them have the form
See also
References
- Cornelius Lanczos, The Variational Principles of Mechanics, Dover (1986), ISBN 0-486-65067-7.
- Iglesias, Patrick, Les origines du calcul symplectique chez Lagrange [The origins of symplectic calculus in Lagrange's work], L'Enseign. Math. (2) 44 (1998), no. 3-4, 257–277. MR 1659212
External links
- Eric W. Weisstein, "Lagrange bracket", MathWorld.
- A.P. Soldatov (2001), "Lagrange bracket", in Hazewinkel, Michiel, Encyclopedia of Mathematics, Springer, ISBN 978-1-55608-010-4
This article is issued from Wikipedia - version of the Monday, May 05, 2014. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.
![[ u, v ]_{p,q} = \sum_{i=1}^n \left(\frac{\partial q_i}{\partial u} \frac{\partial p_i}{\partial v} - \frac{\partial p_i}{\partial u} \frac{\partial q_i}{\partial v} \right).](../I/m/dd67f73d6ddd78bc365bd8ea42079360.png)
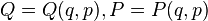
![[ u, v]_{q,p} = [u , v]_{Q,P}](../I/m/8ac1f866eb09a7437f9fcfe509a89136.png)
![[ u_i, u_j ]_{p,q}, \quad 1\leq i,j\leq 2n](../I/m/28de954536fb2c74d8a2d8bd861615b6.png)
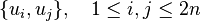
![[Q_i, Q_j]_{p,q}=0, \quad [P_i,P_j]_{p,q}=0,\quad [Q_i, P_j]_{p,q}=-[P_j, Q_i]_{p,q}=\delta_{ij}.](../I/m/fdd581d8b87bc5c4eda2dfff8da8a871.png)