Lévy hierarchy
In set theory and mathematical logic, the Lévy hierarchy, introduced by Azriel Lévy in 1965, is a hierarchy of formulas in the formal language of the Zermelo–Fraenkel set theory, which is typically called just the language of set theory. This is analogous to the arithmetical hierarchy which provides the classifications but for sentences of the language of arithmetic.
Definitions
In the language of set theory, atomic formulas are of the form x = y or x ∈ y, standing for equality and respectively set membership predicates.
The first level of the Levy hierarchy is defined as containing only formulas with no unbounded quantifiers, and is denoted by 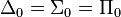 .[1] The next levels are given by finding an equivalent formula in Prenex normal form, and counting the number of changes of quantifiers:
.[1] The next levels are given by finding an equivalent formula in Prenex normal form, and counting the number of changes of quantifiers:
In the theory ZFC, a formula  is called:[1]
is called:[1]
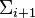 if
if  is equivalent to
is equivalent to 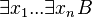 in ZFC, where
in ZFC, where  is
is 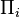
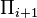 if
if  is equivalent to
is equivalent to 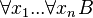 in ZFC, where
in ZFC, where  is
is 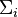
If a formula is both 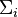 and
and 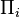 , it is called
, it is called  . As a formula might have several different equivalent formulas in Prenex normal form, it might belong to several different levels of the hierarchy. In this case, the lowest possible level is the level of the formula.
. As a formula might have several different equivalent formulas in Prenex normal form, it might belong to several different levels of the hierarchy. In this case, the lowest possible level is the level of the formula.
The Lévy hierarchy is sometimes defined for other theories S. In this case 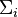 and
and 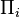 by themselves refer only to formulas that start with a sequence of quantifiers with at most i−1 alternations, and
by themselves refer only to formulas that start with a sequence of quantifiers with at most i−1 alternations, and 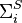 and
and 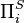 refer to formulas equivalent to
refer to formulas equivalent to 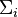 and
and 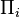 formulas in the theory S. So strictly speaking the levels
formulas in the theory S. So strictly speaking the levels 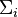 and
and 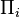 of the Lévy hierarchy for ZFC defined above should be denoted by
of the Lévy hierarchy for ZFC defined above should be denoted by 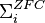 and
and 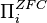 .
.
Examples
Σ0=Π0=Δ0 formulas and concepts
- x = {y, z}
- x ⊆ y
- x is a transitive set
- x is an ordinal, x is a limit ordinal, x is a successor ordinal
- x is a finite ordinal
- The first countable ordinal ω.
- f is a function. The range and domain of a function. The value of a function on a set.
- The product of two sets.
- The union of a set.
Δ1-formulas and concepts
- x is a well-founded relation on y
- x is finite
- Ordinal addition and multiplication and exponentiation
- The rank of a set
- The transitive closure of a set
Σ1-formulas and concepts
- x is countable
- |X|≤|Y|, |X|=|Y|
- x is constructible
Π1-formulas and concepts
- x is a cardinal
- x is a regular cardinal
- x is a limit cardinal
- x is an inaccessible cardinal.
- x is the powerset of y
Δ2-formulas and concepts
- κ is γ-supercompact
Σ2-formulas and concepts
- the Continuum Hypothesis
- there exists an inaccessible cardinal
- there exists a measurable cardinal
- κ is an n-huge cardinal
Π2-formulas and concepts
- The axiom of constructibility: V = L
Δ3-formulas and concepts
Σ3-formulas and concepts
- There is a supercompact cardinal
Π3-formulas and concepts
- κ is an extendible cardinal
Σ4-formulas and concepts
- There is a extendible cardinal
Properties
Jech p. 184 Devlin p. 29
See also
References
- Devlin, Keith J. (1984). Constructibility. Perspectives in Mathematical Logic. Berlin: Springer-Verlag. pp. 27–30. Zbl 0542.03029.
- Jech, Thomas (2003). Set Theory. Springer Monographs in Mathematics (Third Millennium ed.). Berlin, New York: Springer-Verlag. p. 183. ISBN 978-3-540-44085-7. Zbl 1007.03002.
- Kanamori, Akihiro (2006). "Levy and set theory" (PDF). Annals of Pure and Applied Logic 140: 233–252. doi:10.1016/j.apal.2005.09.009. Zbl 1089.03004.
- Levy, Azriel (1965). A hierarchy of formulas in set theory. Mem. Am. Math. Soc. 57. Zbl 0202.30502.