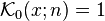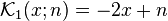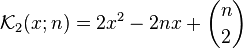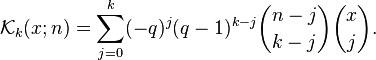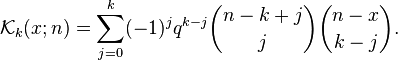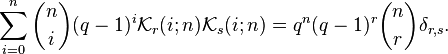Kravchuk polynomials

Kravchuk polynomials or Krawtchouk polynomials (also written using several other transliterations of the Ukrainian name "Кравчу́к") are discrete orthogonal polynomials associated with the binomial distribution, introduced by Mikhail Kravchuk (1929). The first few polynomials are (for q=2):

$\mathcal{K}_0(x; n) = 1$
$\mathcal{K}_1(x; n) = -2x + n$
$\mathcal{K}_2(x; n) = 2x^2 - 2nx + {n\choose 2}$
$\mathcal{K}_3(x; n) = -\frac{4}{3}x^3 + 2nx^2 - (n^2 - n + \frac{2}{3})x + {n \choose 3}.$

The Kravchuk polynomials are a special case of the Meixner polynomials of the first kind.

Definition

For any prime power q and positive integer n, define the Kravchuk polynomial

\mathcal{K}_k(x; n) = \mathcal{K}_k(x) = \sum_{j=0}^{k}(-1)^j (q-1)^{k-j} \binom {x}{j} \binom{n-x}{k-j}, \quad k=0,1, \ldots, n.

Properties

The Kravchuk polynomial has the following alternative expressions:

\mathcal{K}_k(x; n) = \sum_{j=0}^{k}(-q)^j (q-1)^{k-j} \binom {n-j}{k-j} \binom{x}{j}.

\mathcal{K}_k(x; n) = \sum_{j=0}^{k}(-1)^j q^{k-j} \binom {n-k+j}{j} \binom{n-x}{k-j}.

Orthogonality relations

For nonnegative integers r, s,

\sum_{i=0}^n\binom{n}{i}(q-1)^i\mathcal{K}_r(i; n)\mathcal{K}_s(i; n) = q^n(q-1)^r\binom{n}{r}\delta_{r,s}.

References

Kravchuk, M. (1929), "Sur une généralisation des polynomes d'Hermite.", Comptes Rendus Mathematique (in French) 189: 620–622, JFM 55.0799.01
Koornwinder, Tom H.; Wong, Roderick S. C.; Koekoek, Roelof; Swarttouw, René F. (2010), "Hahn Class: Definitions", in Olver, Frank W. J.; Lozier, Daniel M.; Boisvert, Ronald F.; Clark, Charles W., NIST Handbook of Mathematical Functions, Cambridge University Press, ISBN 978-0521192255, MR 2723248
Nikiforov, A. F.; Suslov, S. K.; Uvarov, V. B. (1991), Classical Orthogonal Polynomials of a Discrete Variable, Springer Series in Computational Physics, Berlin: Springer-Verlag, ISBN 3-540-51123-7, MR 1149380 .
Levenshtein, Vladimir I. (1995), "Krawtchouk polynomials and universal bounds for codes and designs in Hamming spaces", IEEE Transactions on Information Theory 41 (5): 1303–1321, doi:10.1109/18.412678, MR 1366326 .
F. J. MacWilliams; N. J. A. Sloane (1977), The Theory of Error-Correcting Codes, North-Holland, ISBN 0-444-85193-3 Cite uses deprecated parameter |coauthors= (help)

External links

This article is issued from Wikipedia - version of the Saturday, January 23, 2016. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.