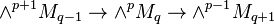Koszul cohomology

In mathematics, the Koszul cohomology groups K_p,q(X, L) are groups associated to a projective variety X with a line bundle L. They were introduced by Green (1984, 1984b), and named after Jean-Louis Koszul as they are closely related to the Koszul complex.

Green (1989) surveys early work on Koszul cohomology, Eisenbud (2005) gives an introduction to Koszul cohomology, and Aprodu & Nagel (2010) gives a more advanced survey.

Definitions

If M is a graded module over the symmetric algebra of a vector space V, then the Koszul cohomology K_p,q(M,V) of M is given by the cohomology of the sequence

\wedge^{p+1}M_{q-1}\rightarrow \wedge^{p}M_{q} \rightarrow \wedge^{p-1}M_{q+1}

If L is a line bundle over a projective variety X, then the Koszul cohomology K_p,q(X,L) is given by the Koszul cohomology K_p,q(M,V) of the graded module M = ⊕_qH⁰(L^q), as a module over the symmetric algebra of the vector space V=H⁰(L).

References

Aprodu, Marian; Nagel, Jan (2010), Koszul cohomology and algebraic geometry, University Lecture Series 52, Providence, R.I.: American Mathematical Society, ISBN 978-0-8218-4964-4, MR 2573635
Eisenbud, David (2005), The geometry of syzygies, Graduate Texts in Mathematics 229, Berlin, New York: Springer-Verlag, doi:10.1007/b137572, ISBN 978-0-387-22215-8, MR 2103875
Green, Mark L. (1984), "Koszul cohomology and the geometry of projective varieties", Journal of Differential Geometry 19 (1): 125–171, ISSN 0022-040X, MR 739785
Green, Mark L. (1984), "Koszul cohomology and the geometry of projective varieties. II", Journal of Differential Geometry 20 (1): 279–289, ISSN 0022-040X, MR 772134
Green, Mark L. (1989), "Koszul cohomology and geometry", in Cornalba, Maurizio; Gómez-Mont, X.; Verjovsky, A., Lectures on Riemann surfaces, Proceedings of the First College on Riemann Surfaces held in Trieste, November 9–December 18, 1987, World Sci. Publ., Teaneck, NJ, pp. 177–200, ISBN 9789971509026, MR 1082354

This article is issued from Wikipedia - version of the Sunday, November 09, 2014. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.