Koopmans' theorem

Koopmans' theorem states that in closed-shell Hartree–Fock theory, the first ionization energy of a molecular system is equal to the negative of the orbital energy of the highest occupied molecular orbital (HOMO). This theorem is named after Tjalling Koopmans, who published this result in 1934.[1] Koopmans became a Nobel laureate in 1975, though neither in physics nor chemistry, but in economics.

Koopmans' theorem is exact in the context of restricted Hartree–Fock theory if it is assumed that the orbitals of the ion are identical to those of the neutral molecule (the frozen orbital approximation). Ionization energies calculated this way are in qualitative agreement with experiment – the first ionization energy of small molecules is often calculated with an error of less than two electron volts.[2][3][4] Therefore, the validity of Koopmans' theorem is intimately tied to the accuracy of the underlying Hartree–Fock wavefunction. The two main sources of error are:

Empirical comparisons with experimental values and higher-quality ab initio calculations suggest that in many cases, but not all, the energetic corrections due to relaxation effects nearly cancel the corrections due to electron correlation.[5][6]

A similar theorem exists in density functional theory (DFT) for relating the exact first vertical ionization energy and electron affinity to the HOMO and LUMO energies, although both the derivation and the precise statement differ from that of Koopmans' theorem. Ionization energies calculated from DFT orbital energies are usually poorer than those of Koopmans' theorem, with errors much larger than two electron volts possible depending on the exchange-correlation approximation employed.[2][3] The LUMO energy shows little correlation with the electron affinity with typical approximations.[7] The error in the DFT counterpart of Koopmans' theorem is a result of the approximation employed for the exchange correlation energy functional so that, unlike in HF theory, there is the possibility of improved results with the development of better approximations.

Generalizations of Koopmans' theorem

While Koopmans' theorem was originally stated for calculating ionization energies from restricted (closed-shell) Hartree–Fock wavefunctions, the term has since taken on a more generalized meaning as a way of using orbital energies to calculate energy changes due to changes in the number of electrons in a system.

Ground-state and excited-state ions

Koopmans’ theorem applies to the removal of an electron from any occupied molecular orbital to form a positive ion. Removal of the electron from different occupied molecular orbitals leads to the ion in different electronic states. The lowest of these states is the ground state and this often, but not always, arises from removal of the electron from the HOMO. The other states are excited electronic states.

For example the electronic configuration of the H2O molecule is (1a1)2 (2a1)2 (1b2)2 (3a1)2 (1b1)2,[8] where the symbols a1, b2 and b1 are orbital labels based on molecular symmetry. From Koopmans’ theorem the energy of the 1b1 HOMO corresponds to the ionization energy to form the H2O+ ion in its ground state (1a1)2 (2a1)2 (1b2)2 (3a1)2 (1b1)1. The energy of the second-highest MO 3a1 refers to the ion in the excited state (1a1)2 (2a1)2 (1b2)2 (3a1)1 (1b1)2, and so on. In this case the order of the ion electronic states corresponds to the order of the orbital energies. Excited-state ionization energies can be measured by photoelectron spectroscopy.

For H2O, the near-Hartree–Fock orbital energies (with sign changed) of these orbitals are 1a1 559.5, 2a1 36.7 1b2 19.5, 3a1 15.9 and 1b1 13.8 eV. The corresponding ionization energies are 539.7, 32.2, 18.5, 14.7 and 12.6 eV.[8] As explained above, the deviations are due to the effects of orbital relaxation as well as differences in electron correlation energy between the molecular and the various ionized states.

For N2 in contrast, the order of orbital energies is not identical to the order of ionization energies. Near-Hartree–Fock calculations with a large basis set indicate that the 1πu bonding orbital is the HOMO. However the lowest ionization energy corresponds to removal of an electron from the 3σg bonding orbital. In this case the deviation is attributed primarily to the difference in correlation energy between the two orbitals.[9]

Koopmans' theorem for electron affinities

It is sometimes claimed[10] that Koopmans' theorem also allows the calculation of electron affinities as the energy of the lowest unoccupied molecular orbitals (LUMO) of the respective systems. However, Koopmans' original paper makes no claim with regard to the significance of eigenvalues of the Fock operator other than that corresponding to the HOMO. Nevertheless, it is straightforward to generalize the original statement of Koopmans' to calculate the electron affinity in this sense.

Calculations of electron affinities using this statement of Koopmans' theorem have been criticized[11] on the grounds that virtual (unoccupied) orbitals do not have well-founded physical interpretations, and that their orbital energies are very sensitive to the choice of basis set used in the calculation. As the basis set becomes more complete; more and more "molecular" orbitals that are not really on the molecule of interest will appear, and care must be taken not to use these orbitals for estimating electron affinities.

Comparisons with experiment and higher-quality calculations show that electron affinities predicted in this manner are generally quite poor.

Koopmans' theorem for open-shell systems

Koopmans' theorem is also applicable to open-shell systems. It was previously believed that this was only in the case for removing the unpaired electron,[12] but the validity of Koopmans’ theorem for ROHF in general has been proven provided that the correct orbital energies are used.[13][14][15][16] The spin up (alpha) and spin down (beta) orbital energies do not necessarily have to be the same.[17]

Counterpart in density functional theory

Kohn–Sham (KS) density functional theory (KS-DFT) admits its own version of Koopmans' theorem (sometimes called the DFT-Koopmans' theorem) very similar in spirit to that of Hartree-Fock theory. The theorem equates the first (vertical) ionization energy I of a system of N electrons to the negative of the corresponding KS HOMO energy \epsilon_H . 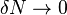More generally, this relation is true even when the KS systems describes a zero-temperature ensemble with non-integer number of electrons N - \delta N for integer N and \delta N \rightarrow 0. When considering N + \delta N electrons the infinitesimal excess charge enters the KS LUMO of the N electron system but then the exact KS potential jumps by a constant known as the "derivative discontinuity".[18] It can be shown that the vertical electron affinity is equal exactly to the negative of the sum of the LUMO energy and the derivative discontinuity.[18][19]

Unlike the approximate status of Koopmans' theorem in Hartree Fock theory (because of the neglect of orbital relaxation), in the exact KS mapping the theorem is exact, including the effect of orbital relaxation. A sketchy proof of this exact relation goes in three stages. First, for any finite system I determines the |\bold{r}|\rightarrow\infty asymptotic form of the density, which decays as n(\bold{r})\rightarrow e^{-2\sqrt{\frac{2 m_e}{\hbar} I}|\bold{r}|}.[18] [20] Next, as a corollary (since the physically interacting system has the same density as the KS system), both must have the same ionization energy. Finally, since the KS potential is zero at infinity, the ionization energy of the KS system is, by definition, the negative of its HOMO energy and thus finally: \epsilon_H = -I , QED.

While these are exact statements in the formalism of DFT, the use of approximate exchange-correlation potentials makes the calculated energies approximate and often the orbital energies are very different from the corresponding ionization energies (even by several eVs!).[21]

A tuning procedure is able to "impose" Koopmans' theorem on DFT approximations thereby improving many of its related predictions in actual applications. [21][22]

In approximate DFTs one can estimate to high degree of accuracy the deviance from Koopmans' theorem using the concept of energy curvature.[23]

References

  1. ↑ Koopmans, Tjalling (1934). "Über die Zuordnung von Wellenfunktionen und Eigenwerten zu den einzelnen Elektronen eines Atoms". Physica (Elsevier) 1 (1–6): 104–113. Bibcode:1934Phy.....1..104K. doi:10.1016/S0031-8914(34)90011-2.
  2. 1 2 Politzer, Peter; Abu-Awwad, Fakher (1998). "A comparative analysis of Hartree–Fock and Kohn–Sham orbital energies". Theoretical Chemistry Accounts: Theory, Computation, and Modeling (Theoretica Chimica Acta) 99 (2): 83–87. doi:10.1007/s002140050307.
  3. 1 2 Hamel, Sebastien; Duffyc, Patrick; Casidad, Mark E.; Salahub, Dennis R. (2002). "Kohn–Sham orbitals and orbital energies: fictitious constructs but good approximations all the same". Journal of Electron Spectroscopy and Related Phenomena 123 (2–3): 345–363. doi:10.1016/S0368-2048(02)00032-4.
  4. ↑ See, for example, Szabo, A.; Ostlund, N. S. "Chapter 3". Modern Quantum Chemistry. ISBN 0-02-949710-8.
  5. ↑ Michl, Josef; Bonačić-Koutecký, Vlasta (1990). Electronic Aspects of Organic Photochemistry. Wiley. p. 35. ISBN 978-0-471-89626-5.
  6. ↑ Hehre, Warren J.; Radom, Leo; Schleyer, Paul v.R.; Pople, John A. (1986). Ab initio molecular orbital theory. Wiley. p. 24. ISBN 0-471-81241-2.
  7. ↑ Zhang, Gang; Musgrave, Charles B. (2007). "Comparison of DFT Methods for Molecular Orbital Eigenvalue Calculations". The Journal of Physical Chemistry A 111 (8): 1554–1561. doi:10.1021/jp061633o. PMID 17279730.
  8. 1 2 Levine, I. N. (1991). Quantum Chemistry (4th ed.). Prentice-Hall. p. 475. ISBN 0-7923-1421-2.
  9. ↑ Duke, Brian J.; O'Leary, Brian (1995). "Non-Koopmans' Molecules". Journal of Chemical Education 72 (6): 501. Bibcode:1995JChEd..72..501D. doi:10.1021/ed072p501.
  10. ↑ See, for example, Szabo, A.; Ostlund, N. S. Modern Quantum Chemistry. p. 127. ISBN 0-02-949710-8.
  11. ↑ Jensen, Frank (1990). Introduction to Computational Chemistry. Wiley. pp. 64–65. ISBN 0-471-98425-6.
  12. ↑ Fulde, Peter (1995). Electron correlations in molecules and solids. Springer. pp. 25–26. ISBN 3-540-59364-0.
  13. ↑ Plakhutin, B. N.; Gorelik, E. V.; Breslavskaya, N. N. (2006). "Koopmans' theorem in the ROHF method: Canonical form for the Hartree-Fock Hamiltonian". The Journal of Chemical Physics 125 (20): 204110. Bibcode:2006JChPh.125t4110P. doi:10.1063/1.2393223. PMID 17144693.
  14. ↑ Davidson, Ernest R.; Plakhutin, Boris N. (2010). "Koopmans's theorem in the restricted open-shell Hartree–Fock method. II. The second canonical set for orbitals and orbital energies". The Journal of Chemical Physics 132 (18): 184110. Bibcode:2010JChPh.132r4110D. doi:10.1063/1.3418615.
  15. ↑ Plakhutin, Boris N.; Davidson, Ernest R. (2009). "Koopmans' Theorem in the Restricted Open-Shell Hartree−Fock Method. 1. A Variational Approach†". The Journal of Physical Chemistry A 113 (45): 12386–12395. Bibcode:2009JPCA..11312386P. doi:10.1021/jp9002593. PMID 19459641.
  16. ↑ Glaesemann, Kurt R.; Schmidt, Michael W. (2010). "On the Ordering of Orbital Energies in High-Spin ROHF†". The Journal of Physical Chemistry A 114 (33): 8772–8777. doi:10.1021/jp101758y. PMID 20443582.
  17. ↑ Tsuchimochi, Takashi; Scuseria, Gustavo E. (2010). "Communication: ROHF theory made simple". The Journal of Chemical Physics 133 (14): 141102. arXiv:1008.1607. Bibcode:2010JChPh.133n1102T. doi:10.1063/1.3503173. PMID 20949979.
  18. 1 2 3 Perdew, John P.; Parr, Robert G.; Levy, Mel; Balduz, Jr., Jose L. (1982). "Density-Functional Theory for Fractional Particle Number: Derivative Discontinuities of the Energy". Physical Review Letters 49 (23): 1691–1694. Bibcode:1982PhRvL..49.1691P. doi:10.1103/PhysRevLett.49.1691.
  19. ↑ Perdew, John P.; Levy, Mel (1997). "Comment on "Significance of the highest occupied Kohn–Sham eigenvalue"". Physical Review B 56 (24): 16021–16028. Bibcode:1997PhRvB..5616021P. doi:10.1103/PhysRevB.56.16021.
  20. ↑ Almbladh, C. -O.; von Barth, U. (1985). "Exact results for the charge and spin densities, exchange-correlation potentials, and density-functional eigenvalues". Physical Review B 31 (6): 3231. Bibcode:1985PhRvB..31.3231A. doi:10.1103/PhysRevB.31.3231.
  21. 1 2 Salzner, U.; Baer, R. (2009). "Koopmans' springs to life". The Journal of Chemical Physics 131 (23): 231101–4. Bibcode:2009JChPh.131w1101S. doi:10.1063/1.3269030.
  22. ↑ Baer, R.; Livshits, E.; Salzner, U. (2010). ""Tuned" Range-separated hybrids in density functional theory". Annual Review of Physical Chemistry 61: 85–109. doi:10.1146/annurev.physchem.012809.103321. PMID 20055678.Stein, T.; Eisenberg, H.; Kronik, L.; Baer, R. (2010). "Fundamental gaps of finite systems from the eigenvalues of a generalized Kohn-Sham method". Physical Review Letters 105 (26): 266802. arXiv:1006.5420. Bibcode:2010PhRvL.105z6802S. doi:10.1103/PhysRevLett.105.266802. PMID 21231698. Kornik, L.; Stein, T.; Refaely-Abramson, S.; Baer, R. (2012). "Excitation Gaps of Finite-Sized Systems from Optimally Tuned Range-Separated Hybrid Functionals". Journal of Chemical Theory and Computation 8 (5): 1515. doi:10.1021/ct2009363.
  23. ↑ Stein, Tamar; Autschbach, Jochen; Govind, Niranjan; Kronik, Leeor; Baer, Roi (2012). "Curvature and frontier orbital energies in density functional theory". The Journal of Physical Chemistry Letters 3 (24): 3740. arXiv:1208.1496. doi:10.1021/jz3015937.

External links

This article is issued from Wikipedia - version of the Tuesday, February 02, 2016. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.