Koopman–von Neumann classical mechanics
The Koopman–von Neumann mechanics is a description of classical mechanics in terms of Hilbert space, introduced by Bernard Koopman and John von Neumann in 1931 and 1932. [1] [2] [3]
As Koopman and von Neumann demonstrated, a Hilbert space of complex, square integrable wavefunctions can be defined in which classical mechanics can be formulated as an operatorial theory similar to quantum mechanics.
History
The origins of Koopman–von Neumann (KvN) theory are tightly connected with the rise of ergodic theory as an independent branch of mathematics, in particular with Boltzmann's ergodic hypothesis which plays a crucial role in theoretical physics, more specifically, for describing systems of statistical mechanics in terms of statistical ensembles. For instance, the macroscopic properties of the ideal gas can thus be explained from microscopic mechanics of individual atoms and molecules.
In 1931 Koopman and André Weil independently observed that the phase space of the classical system can be converted into a Hilbert space by postulating a natural integration rule over the points of the phase space as the definition of the scalar product, and that this transformation allows drawing of interesting conclusions about the evolution of physical observables from Stone's theorem, which had been proved shortly before. This finding inspired von Neumann to apply the novel formalism to the ergodic problem. Already in 1932 he completed the operator reformulation of quantum mechanics currently known as Koopman–von Neumann theory. Subsequently he published several seminal results in modern ergodic theory including the proof of his mean ergodic theorem.
Definition and dynamics
Derivation starting from the Liouville equation
In the approach of Koopman and von Neumann (KvN), dynamics in phase space is described by a (classical) probability density, recovered from an underlying wavefunction – the Koopman–von Neumann wavefunction – as the square of its absolute value (more precisely, as the amplitude multiplied with its own complex conjugate). This stands in analogy to the Born rule in quantum mechanics. In the KvN framework, observables are represented by commuting self-adjoint operators acting on the Hilbert space of KvN wavefunctions. The commutativity physically implies that all observables are simultaneously measurable. Contrast this with quantum mechanics, where observables need not commute, which underlines the uncertainty principle, Kochen–Specker theorem, and Bell inequalities.[4]
The KvN wavefunction is postulated to evolve according to exactly the same Liouville equation as the classical probability density. From this postulate it can be shown that indeed probability density dynamics is recovered.
Derivation starting from operator axioms
Conversely, it is possible to start from operator postulates, similar to the Hilbert space axioms of quantum mechanics, and derive the equation of motion by specifying how expectation values evolve.[7]
The relevant axioms are that as in quantum mechanics (i) the states of a system are represented by normalized vectors of a complex Hilbert space, and the observables are given by self-adjoint operators acting on that space, (ii) the expectation value of an observable is obtained in the manner as the expectation value in quantum mechanics, (iii) the probabilities of measuring certain values of some observables are calculated by the Born rule, and (iv) the state space of a composite system is the tensor product of the subsystem's spaces.
These axioms allow us to recover the formalism of both classical and quantum mechanics.[7] Specifically, under the assumption that the classical position and momentum operators commute, the Liouville equation for the KvN wavefunction is recovered from averaged Newton's laws of motion. However, if the coordinate and momentum obey the canonical commutation relation, the Schrödinger equation of quantum mechanics is obtained.
Measurements
In the Hilbert space and operator formulation of classical mechanics, the Koopman von Neumann–wavefunction takes the form of a superposition of eigenstates, and measurement collapses the KvN wavefunction to the eigenstate which is associated the measurement result, in analogy to the wave function collapse of quantum mechanics.
However, it can be shown that for Koopman–von Neumann classical mechanics non-selective measurements leave the KvN wavefunction unchanged.[5]
KvN vs Liouville mechanics
The KvN dynamical equation (KvN dynamical eq in xp) and Liouville equation (Liouville eq) are first-order linear partial differential equations. One recovers Newton's laws of motion by applying the method of characteristics to either of these equations. Hence, the key difference between KvN and Liouville mechanics lies in weighting individual trajectories: Arbitrary weights, underlying the classical wave function, can be utilized in the KvN mechanics, while only positive weights, representing the probability density, are permitted in the Liouville mechanics (see this scheme).
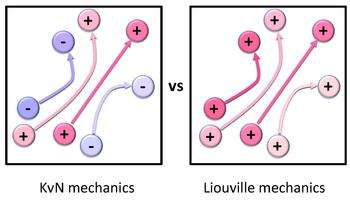
Quantum analogy
Being explicitly based on the Hilbert space language, the KvN classical mechanics adopts many techniques from quantum mechanics, for example, perturbation and diagram techniques [18] as well as functional integral methods [19] [20] .[21] The KvN approach is very general, and it has been extended to dissipative systems,[22] relativistic mechanics,[23] and classical field theories [7] [24] [25] .[26]
The KvN approach is fruitful in studies on the quantum-classical correspondence [7] [8] [27] [28] [29] as it reveals that the Hilbert space formulation is not exclusively quantum mechanical. Even Dirac spinors are not exceptionally quantum as they are utilized in the relativistic generalization of the KvN mechanics.[23] Similarly as the more well-known phase space formulation of quantum mechanics, the KvN approach can be understood as an attempt to bring classical and quantum mechanics into a common mathematical framework. In fact, the time evolution of the Wigner function approaches, in the classical limit, the time evolution of the KvN wavefunction of a classical particle. [23] [30] However, a mathematical resemblance to quantum mechanics does not imply the presence of hallmark quantum effects. In particular, impossibility of double-slit experiment[6][10][11] and Aharonov–Bohm effect[12] are explicitly demonstrated in the KvN framework.
| KvN propagation vs Wigner propagation | ||||
|---|---|---|---|---|
|
See also
- Classical mechanics
- Liouville's theorem
- Quantum mechanics
- Phase space formulation of quantum mechanics
- Wigner quasiprobability distribution
- Dynamical systems
- Ergodic theory
References
- ↑ Koopman, B. O. (1931). "Hamiltonian Systems and Transformations in Hilbert Space". Proceedings of the National Academy of Sciences 17 (5): 315. doi:10.1073/pnas.17.5.315.
- ↑ von Neumann, J. (1932). "Zur Operatorenmethode In Der Klassischen Mechanik". Annals of Mathematics 33 (3): 587–642. doi:10.2307/1968537. JSTOR 1968537.
- ↑ von Neumann, J. (1932). "Zusatze Zur Arbeit "Zur Operatorenmethode..."". Annals of Mathematics 33 (4): 789–791. doi:10.2307/1968225. JSTOR 1968225.
- ↑ Landau, L. J. (1987). "On the violation of Bell's inequality in quantum theory". Physics Letters A 120 (2): 54–39. Bibcode:1987PhLA..120...54L. doi:10.1016/0375-9601(87)90075-2.
- 1 2 3 Mauro, D. (2002). "Topics in Koopman–von Neumann Theory". arXiv:quant-ph/0301172 [quant-ph]. PhD thesis, Università degli Studi di Trieste.
- 1 2 3 4 Mauro, D. (2002). "On Koopman–Von Neumann Waves". International Journal of Modern Physics A 17 (9): 1301. arXiv:quant-ph/0105112. Bibcode:2002IJMPA..17.1301M. doi:10.1142/S0217751X02009680.
- 1 2 3 4 5 6 Bondar, D.; Cabrera, R.; Lompay, R.; Ivanov, M.; Rabitz, H. (2012). "Operational Dynamic Modeling Transcending Quantum and Classical Mechanics". Physical Review Letters 109 (19). arXiv:1105.4014. Bibcode:2012PhRvL.109s0403B. doi:10.1103/PhysRevLett.109.190403.
- 1 2 Brumer, P.; Gong, J. (2006). "Born rule in quantum and classical mechanics". Physical Review A 73 (5). arXiv:quant-ph/0604178. Bibcode:2006PhRvA..73e2109B. doi:10.1103/PhysRevA.73.052109.
- 1 2 Transtrum, M. K.; Van Huele, J. F. O. S. (2005). "Commutation relations for functions of operators". Journal of Mathematical Physics 46 (6): 063510. Bibcode:2005JMP....46f3510T. doi:10.1063/1.1924703.
- 1 2 Gozzi, E.; Mauro, D. (2004). "On Koopman–Von Neumann Waves Ii". International Journal of Modern Physics A 19 (9): 1475. arXiv:quant-ph/0306029. Bibcode:2004IJMPA..19.1475G. doi:10.1142/S0217751X04017872.
- 1 2 Gozzi, E.; Pagani, C. (2010). "Universal Local Symmetries and Nonsuperposition in Classical Mechanics". Physical Review Letters 105 (15). arXiv:1006.3029. Bibcode:2010PhRvL.105o0604G. doi:10.1103/PhysRevLett.105.150604.
- 1 2 Gozzi, E.; Mauro, D. (2002). "Minimal Coupling in Koopman–von Neumann Theory". Annals of Physics 296 (2): 152. arXiv:quant-ph/0105113. Bibcode:2002AnPhy.296..152G. doi:10.1006/aphy.2001.6206.
- 1 2 Blokhintsev, D. I. (1977). "Classical statistical physics and quantum mechanics". Soviet Physics Uspekhi 20 (8): 683. doi:10.1070/PU1977v020n08ABEH005457.
- ↑ Blokhintsev, D.I. (1940). "The Gibbs Quantum Ensemble and its Connection with the Classical Ensemble". J. Phys. U.S.S.R. 2 (1): 71–74.
- ↑ Blokhintsev, D.I.; Nemirovsky, P (1940). "Connection of the Quantum Ensemble with the Gibbs Classical Ensemble. II". J. Phys. U.S.S.R. 3 (3): 191–194.
- ↑ Blokhintsev, D.I.; Dadyshevsky, Ya. B. (1941). "On Separation of a System into Quantum and Classical Parts". Zh. Eksp. Teor. Fiz. 11 (2–3): 222–225.
- ↑ Blokhintsev, D.I. (2010). The Philosophy of Quantum Mechanics. Springer. ISBN 9789048183357.
- ↑ Liboff, R. L. (2003). Kinetic theory: classical, quantum, and relativistic descriptions. Springer. ISBN 9780387955513.
- ↑ Gozzi, E. (1988). "Hidden BRS invariance in classical mechanics". Physics Letters B 201 (4): 525–528. Bibcode:1988PhLB..201..525G. doi:10.1016/0370-2693(88)90611-9.
- ↑ Gozzi, E.; Reuter, M.; Thacker, W. (1989). "Hidden BRS invariance in classical mechanics. II". Physical Review D 40 (10): 3363. Bibcode:1989PhRvD..40.3363G. doi:10.1103/PhysRevD.40.3363.
- ↑ Blasone, M.; Jizba, P.; Kleinert, H. (2005). "Path-integral approach to 't Hooft's derivation of quantum physics from classical physics". Physical Review A 71 (5). arXiv:quant-ph/0409021. Bibcode:2005PhRvA..71e2507B. doi:10.1103/PhysRevA.71.052507.
- ↑ Chruściński, D. (2006). "Koopman's approach to dissipation". Reports on Mathematical Physics 57 (3): 319–332. doi:10.1016/S0034-4877(06)80023-6.
- 1 2 3 Renan Cabrera; Bondar; Rabitz (2011). "Relativistic Wigner function and consistent classical limit for spin 1/2 particles". arXiv:1107.5139 [quant-ph].
- ↑ Carta, P.; Gozzi, E.; Mauro, D. (2006). "Koopman–von Neumann formulation of classical Yang–Mills theories: I". Annalen der Physik 15 (3): 177. arXiv:hep-th/0508244. Bibcode:2006AnP...518..177C. doi:10.1002/andp.200510177.
- ↑ Gozzi, E.; Penco, R. (2011). "Three approaches to classical thermal field theory". Annals of Physics 326 (4): 876. arXiv:1008.5135. Bibcode:2011AnPhy.326..876G. doi:10.1016/j.aop.2010.11.018.
- ↑ Cattaruzza, E.; Gozzi, E.; Francisco Neto, A. (2011). "Diagrammar in classical scalar field theory". Annals of Physics 326 (9): 2377. arXiv:1010.0818. Bibcode:2011AnPhy.326.2377C. doi:10.1016/j.aop.2011.05.009.
- ↑ Wilkie, J.; Brumer, P. (1997). "Quantum-classical correspondence via Liouville dynamics. I. Integrable systems and the chaotic spectral decomposition". Physical Review A 55: 27. Bibcode:1997PhRvA..55...27W. doi:10.1103/PhysRevA.55.27.
- ↑ Wilkie, J.; Brumer, P. (1997). "Quantum-classical correspondence via Liouville dynamics. II. Correspondence for chaotic Hamiltonian systems". Physical Review A 55: 43. Bibcode:1997PhRvA..55...43W. doi:10.1103/PhysRevA.55.43.
- ↑ Abrikosov, A. A.; Gozzi, E.; Mauro, D. (2005). "Geometric dequantization". Annals of Physics 317: 24. arXiv:quant-ph/0406028. Bibcode:2005AnPhy.317...24A. doi:10.1016/j.aop.2004.12.001.
- ↑ Bondar; Renan Cabrera; Zhdanov; Rabitz (2012). "Wigner Function's Negativity Demystified". arXiv:1202.3628 [quant-ph].
Further reading
- Mauro, D. (2002). "Topics in Koopman–von Neumann Theory". arXiv:quant-ph/0301172 [quant-ph]. PhD thesis, Università degli Studi di Trieste.
- H.R. Jauslin, D. Sugny, Dynamics of mixed classical-quantum systems, geometric quantization and coherent states, Lecture Note Series, IMS, NUS, Review Vol., August 13, 2009
- The Legacy of John von Neumann (Proceedings of Symposia in Pure Mathematics, vol 50), edited by James Glimm, John Impagliazzo, Isadore Singer. — Amata Graphics, 2006. — ISBN 0821842196
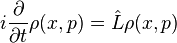
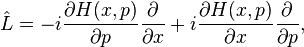
 denotes the
denotes the 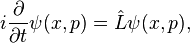
![\frac{\partial}{\partial t} \psi(x, p) = \left[- \frac{\partial H(x, p)}{\partial p} \frac{\partial}{\partial x} + \frac{\partial H(x, p)}{\partial x} \frac{\partial}{\partial p} \right] \psi(x, p),](../I/m/962a31c164e8e393a9b5b461eb06438e.png)
![\frac{\partial}{\partial t} \psi^*(x, p) = \left[- \frac{\partial H(x, p)}{\partial p} \frac{\partial}{\partial x} + \frac{\partial H(x, p)}{\partial x} \frac{\partial}{\partial p} \right] \psi^*(x, p).](../I/m/cad9993e709caa734cd8e70f322ab948.png)
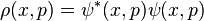
![\frac{\partial}{\partial t} \rho(x, p) = \left[- \frac{\partial H(x, p)}{\partial p} \frac{\partial}{\partial x} + \frac{\partial H(x, p)}{\partial x} \frac{\partial}{\partial p} \right] \rho(x, p)](../I/m/d20e45826e508ef7bb4663fe595c2c04.png)
 ,
,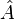 at time
at time  is
is 
 is
is  , where
, where 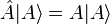 . (This axiom is an analogue of the
. (This axiom is an analogue of the 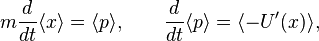
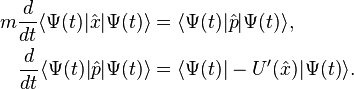
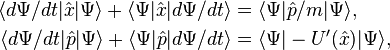
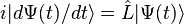 and obtain
and obtain![\begin{align}
im \langle \Psi(t) | [\hat{L}, \hat{x} ] | \Psi(t) \rangle &= \langle \Psi(t)| \hat{p} |\Psi(t)\rangle, \\
i \langle \Psi(t) | [\hat{L}, \hat{p}] | \Psi(t)\rangle &= - \langle \Psi(t)| U'(\hat{x}) |\Psi(t)\rangle.
\end{align}](../I/m/fda25d6bb650fb86e4077b0037c02749.png)
 is derived
is derived![im [\hat{L}, \hat{x}] = \hat{p} , \qquad i [\hat{L}, \hat{p}] = -U'(\hat{x}).](../I/m/8ff3023bfbbb09feedc294799a42f272.png)
![[ \hat{x}, \hat{p} ] = 0](../I/m/0febed3dbe141fa01103ce9643aaf3fe.png) . This assumption physically means that the classical particle's coordinate and momentum can be measured simultaneously, implying absence of the
. This assumption physically means that the classical particle's coordinate and momentum can be measured simultaneously, implying absence of the 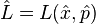 because it would imply the contractions
because it would imply the contractions ![im [L(\hat{x}, \hat{p}), \hat{x}] = 0 = \hat{p}](../I/m/1a1177ea4ea56ffe60cbce0891f84554.png) and
and ![i [L(\hat{x}, \hat{p}), \hat{p}] = 0 = -U'(\hat{x})](../I/m/96859519b5815e3734531297e1625bd0.png) . Therefore, we must utilize additional operators
. Therefore, we must utilize additional operators 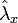 and
and 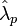 obeying
obeying![[ \hat{x}, \hat{\lambda}_x ] = [ \hat{p}, \hat{\lambda}_p ] = i, \quad [\hat{x}, \hat{p}] = [ \hat{x}, \hat{\lambda}_p ] = [ \hat{p}, \hat{\lambda}_x ] = [ \hat{\lambda}_x, \hat{\lambda}_p ] = 0.](../I/m/527035888f3782a07b6d70b4cf2b8f62.png)
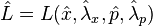 . Utilizing
. Utilizing 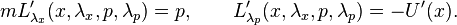
 evolves according to the
evolves according to the 
 and
and  commute, they share the common
commute, they share the common 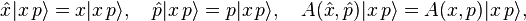
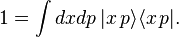 Then, one obtains from equation (
Then, one obtains from equation (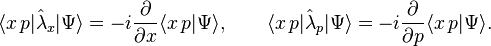
 , we get the equation of motion for the KvN wave function in the xp-representation
, we get the equation of motion for the KvN wave function in the xp-representation![\left[ \frac{\partial }{\partial t} + \frac{p}{m} \frac{\partial}{\partial x} - U'(x) \frac{\partial}{\partial p} \right] \langle x \, p | \Psi(t) \rangle = 0.](../I/m/be8edadaa5761adcf2704d692d85189d.png)
 is the probability amplitude for a classical particle to be at point
is the probability amplitude for a classical particle to be at point  with momentum
with momentum  at time
at time 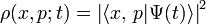 . Utilizing the identity
. Utilizing the identity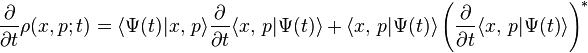
![\left[ \frac{\partial }{\partial t} + \frac{p}{m} \frac{\partial}{\partial x} - U'(x) \frac{\partial}{\partial p} \right] \rho(x,p;t) = 0.](../I/m/51d8c3918cd66569e887a71a045a9f39.png)
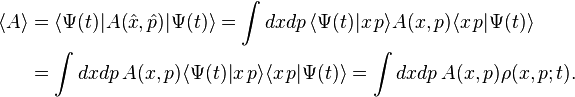
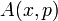 in classical statistical mechanics has been recovered from the
in classical statistical mechanics has been recovered from the 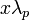 -representation), one obtains classical mechanics in the doubled configuration space,
-representation), one obtains classical mechanics in the doubled configuration space,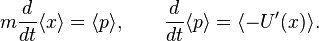
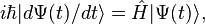
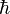 was introduced as a normalization constant to balance dimensionality. Since these identities must be valid for any initial state, the averaging can be dropped and the system of commutator equations for the unknown quantum generator of motion
was introduced as a normalization constant to balance dimensionality. Since these identities must be valid for any initial state, the averaging can be dropped and the system of commutator equations for the unknown quantum generator of motion 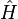 are derived
are derived![im [\hat{H}, \hat{x}] = \hbar \hat{p}, \qquad i [\hat{H}, \hat{p}] = -\hbar U'(\hat{x}).](../I/m/1f2675a9ac117e8902f73efde22cced7.png)
![[ \hat{x}, \hat{p} ] = i\hbar](../I/m/48027576a2df700499372764cdaedfc7.png) . Setting
. Setting 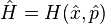 , the commutator equations can be converted into the differential equations
, the commutator equations can be converted into the differential equations

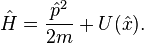
![[ \hat{x}, \hat{p} ]](../I/m/cb0373d65ea52c5f2696106cc7a2ab22.png) .
.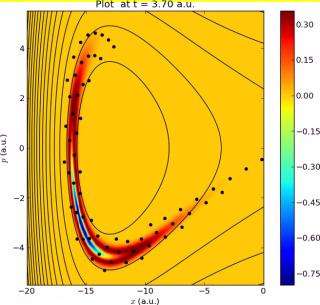
 . Black dots are classical particles following
. Black dots are classical particles following 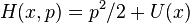 . This video illustrates
. This video illustrates 