Kolmogorov's inequality
In probability theory, Kolmogorov's inequality is a so-called "maximal inequality" that gives a bound on the probability that the partial sums of a finite collection of independent random variables exceed some specified bound. The inequality is named after the Russian mathematician Andrey Kolmogorov.
Statement of the inequality
Let X1, ..., Xn : Ω → R be independent random variables defined on a common probability space (Ω, F, Pr), with expected value E[Xk] = 0 and variance Var[Xk] < +∞ for k = 1, ..., n. Then, for each λ > 0,
where Sk = X1 + ... + Xk.
Proof
The following argument is due to Kareem Amin and employs discrete martingales.
As argued in the discussion of Doob's martingale inequality, the sequence 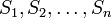 is a martingale.
Without loss of generality, we can assume that
is a martingale.
Without loss of generality, we can assume that 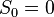 and
and 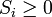 for all
for all  .
Define
.
Define 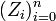 as follows. Let
as follows. Let 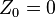 , and
, and
for all  .
Then
.
Then 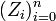 is also a martingale. Since
is also a martingale. Since 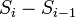 is independent and mean zero,
is independent and mean zero,
The same is true for 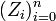 . Thus
. Thus
This inequality was generalized by Hájek and Rényi in 1955.
See also
- Chebyshev's inequality
- Etemadi's inequality
- Landau–Kolmogorov inequality
- Markov's inequality
- Bernstein inequalities (probability theory)
References
- Billingsley, Patrick (1995). Probability and Measure. New York: John Wiley & Sons, Inc. ISBN 0-471-00710-2. (Theorem 22.4)
- Feller, William (1968) [1950]. An Introduction to Probability Theory and its Applications, Vol 1 (Third ed.). New York: John Wiley & Sons, Inc. xviii+509. ISBN 0-471-25708-7.
This article incorporates material from Kolmogorov's inequality on PlanetMath, which is licensed under the Creative Commons Attribution/Share-Alike License.
![\Pr \left(\max_{1\leq k\leq n} | S_k |\geq\lambda\right)\leq \frac{1}{\lambda^2} \operatorname{Var} [S_n] \equiv \frac{1}{\lambda^2}\sum_{k=1}^n \operatorname{Var}[X_k],](../I/m/a3ffdadd6604c7b0ced74edbd6c81302.png)
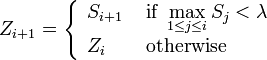
![\begin{align}
\sum_{i=1}^n \text{E}[ (S_i - S_{i-1})^2] &= \sum_{i=1}^n \text{E}[ S_i^2 - 2 S_i S_{i-1} + S_{i-1}^2 ] \\
&= \sum_{i=1}^n \text{E}\left[ S_i^2 - 2 (S_{i-1} + S_{i} - S_{i-1}) S_{i-1} + S_{i-1}^2 \right] \\
&= \sum_{i=1}^n \text{E}\left[ S_i^2 - S_{i-1}^2 \right] - 2\text{E}\left[ S_{i-1} (S_{i}-S_{i-1})\right]\\
&= \text{E}[S_n^2] - \text{E}[S_0^2] = \text{E}[S_n^2].
\end{align}](../I/m/755539cbc71aa8be59c92a7c25115050.png)
![\begin{align}
\text{Pr}\left( \max_{1 \leq i \leq n} S_i \geq \lambda\right) &=
\text{Pr}[Z_n \geq \lambda] \\
&\leq \frac{1}{\lambda^2} \text{E}[Z_n^2]
=\frac{1}{\lambda^2} \sum_{i=1}^n \text{E}[(Z_i - Z_{i-1})^2] \\
&\leq \frac{1}{\lambda^2} \sum_{i=1}^n \text{E}[(S_i - S_{i-1})^2]
=\frac{1}{\lambda^2} \text{E}[S_n^2] = \frac{1}{\lambda^2} \text{Var}[S_n]
\end{align}](../I/m/8b6035cd295c5a7b0adb528f8b4f7db7.png)