Knot polynomial
.svg.png)
In the mathematical field of knot theory, a knot polynomial is a knot invariant in the form of a polynomial whose coefficients encode some of the properties of a given knot.
History
The first knot polynomial, the Alexander polynomial, was introduced by James Waddell Alexander II in 1923, but other knot polynomials were not found until almost 60 years later.
In the 1960s, John Conway came up with a skein relation for a version of the Alexander polynomial, usually referred to as the Alexander–Conway polynomial. The significance of this skein relation was not realized until the early 1980s, when Vaughan Jones discovered the Jones polynomial. This led to the discovery of more knot polynomials, such as the so-called HOMFLY polynomial.
Soon after Jones' discovery, Louis Kauffman noticed the Jones polynomial could be computed by means of a state-sum model, which involved the bracket polynomial, an invariant of framed knots. This opened up avenues of research linking knot theory and statistical mechanics.
In the late 1980s, two related breakthroughs were made. Edward Witten demonstrated that the Jones polynomial, and similar Jones-type invariants, had an interpretation in Chern–Simons theory. Viktor Vassiliev and Mikhail Goussarov started the theory of finite type invariants of knots. The coefficients of the previously named polynomials are known to be of finite type (after perhaps a suitable "change of variables").
In recent years, the Alexander polynomial has been shown to be related to Floer homology. The graded Euler characteristic of the knot Floer homology of Ozsváth and Szabó is the Alexander polynomial.
Example
| Alexander–Briggs notation | Alexander polynomial  | Conway polynomial  | Jones polynomial  | HOMFLY polynomial  |
|---|---|---|---|---|
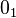 (Unknot) (Unknot) | 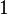 | 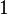 | 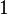 | 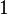 |
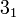 (Trefoil Knot) (Trefoil Knot) | 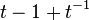 | 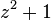 | 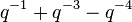 | 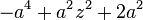 |
 (Figure-eight Knot) (Figure-eight Knot) | 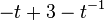 | 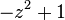 |  | 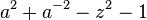 |
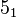 (Cinquefoil Knot) (Cinquefoil Knot) | 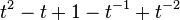 | 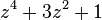 | 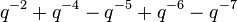 | 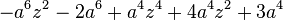 |
 (Granny Knot) (Granny Knot) | 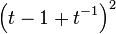 | 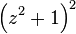 |  | 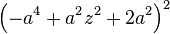 |
 (Square Knot) (Square Knot) | 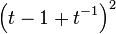 | 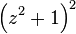 | 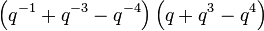 |  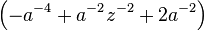 |
Alexander–Briggs notation is a notation that simply organizes knots by their crossing number. The order of Alexander–Briggs notation of prime knot is usually sured. (See List of prime knots.)
Notice that Alexander polynomial and Conway polynomial can not recognize the difference of left-trefoil knot and right-trefoil knot.
-

The left-trefoil knot.
-

The right-trefoil knot.
So the same situation as granny knot and square knot,since the addition of knots in 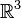 is the product of knots in knot polynomials.
is the product of knots in knot polynomials.
See also
Specific knot polynomials
Related topics
- skein relationship for a formal definition of the Alexander polynomial, with a worked-out example.
Further reading
- Colin Adams, The Knot Book, American Mathematical Society, ISBN 0-8050-7380-9
- W. B. R. Lickorish, An introduction to knot theory. Graduate Texts in Mathematics, 175. Springer-Verlag, New York, 1997. ISBN 0-387-98254-X
| ||||||||||||||||||||||||||||||