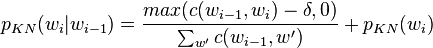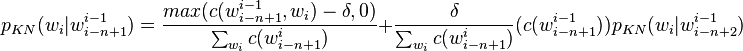Kneser–Ney smoothing

Kneser–Ney smoothing is a method primarily used to calculate the probability distribution of n-grams in a document based on their histories.[1] It is widely considered the most effective method of smoothing due to its use of absolute discounting by subtracting a fixed value from the probability's lower order terms to omit n-grams with lower frequencies. This approach has been considered equally effective for both higher and lower order n-grams.

A common example that illustrates the concept behind this method is the frequency of the bigram "San Francisco". If it appears several times in a training corpus, the frequency of the unigram "Francisco" will also be high. Relying on only the unigram frequency to predict the frequencies of n-grams leads to skewed results;[2] however, Kneser–Ney smoothing corrects this by considering the frequency of the unigram in relation to possible words preceding it.

Method

The equation for bigram probabilities are as follows:

p_{KN}(w_i|w_{i-1}) = \frac{max(c(w_{i-1},w_{i}) - \delta,0)}{\sum_{w'} c(w_{i-1},w')} + p_{KN}(w_i) [3]

This equation can be extended to n-grams:

p_{KN}(w_i|w_{i-n+1}^{i-1}) = \frac{max(c(w_{i-n+1}^{i-1},w_{i}) - \delta,0)}{\sum_{w_i} c(w_{i-n+1}^{i})} + \frac{\delta}{\sum_{w_i} c(w_{i-n+1}^{i})} (c(w_{i-n+1}^{i-1}))p_{KN}(w_i|w_{i-n+2}^{i-1}) [4]


The probability 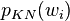p_{KN}(w_i) for a single word is the number of times it appears after any other word divided by the number of words in the corpus, which is represented by the function 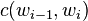c(w_{i-1},w_{i}). The parameter 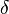\delta is a constant which denotes the discount value subtracted from the count of each n-gram, usually between 0 and 1. This model uses the concept of absolute-discounting interpolation which incorporates information from higher and lower order language models. The addition of the term for lower order n-grams adds more weight to the overall probability when the count for the higher order n-grams is zero.[5] Similarly, the weight of the lower order model decreases when the count of the n-gram is non zero.

References

  1. ↑ 'A Bayesian Interpretation of Interpolated Kneser-Ney NUS School of Computing Technical Report TRA2/06'
  2. ↑ 'Brown University: Introduction to Computational Linguistics '
  3. ↑ 'Kneser Ney Smoothing Explained'
  4. ↑ 'NLP Tutorial: Smoothing'
  5. ↑ 'An empirical study of smoothing techniques for language modeling'


This article is issued from Wikipedia - version of the Wednesday, October 07, 2015. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.