Knaster–Kuratowski fan
In topology, a branch of mathematics, the Knaster–Kuratowski fan (also known as Cantor's leaky tent or Cantor's teepee depending on the presence or absence of the apex) is a connected topological space with the property that the removal of a single point makes it totally disconnected.
Let 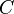 be the Cantor set, let
be the Cantor set, let  be the point
be the point 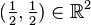 , and let
, and let 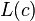 , for
, for 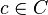 , denote the line segment connecting
, denote the line segment connecting 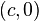 to
to  . If
. If 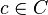 is an endpoint of an interval deleted in the Cantor set, let
is an endpoint of an interval deleted in the Cantor set, let 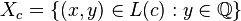 ; for all other points in
; for all other points in 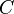 let
let 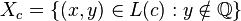 ; the Knaster–Kuratowski fan is defined as
; the Knaster–Kuratowski fan is defined as 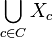 equipped with the subspace topology inherited from the standard topology on
equipped with the subspace topology inherited from the standard topology on 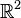 .
.
The fan itself is connected, but becomes totally disconnected upon the removal of  .
.
References
- Knaster, B.; Kuratowski, C. (1921), "Sur les ensembles connexes" (PDF), Fundamenta Mathematicae 2 (1): 206–255
- Steen, Lynn Arthur; Seebach, J. Arthur Jr. (1995) [1978], Counterexamples in Topology (Dover reprint of 1978 ed.), Berlin, New York: Springer-Verlag, ISBN 978-0-486-68735-3, MR 507446
External links
This article is issued from Wikipedia - version of the Friday, February 20, 2015. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.
