Knödel number
In number theory, a Knödel number for a given positive integer n is a composite number m with the property that each i < m coprime to m satisfies 
. The concept is named after Walter Knödel.[1] The set of all Knödel numbers for n is denoted Kn.
The special case K1 are the Carmichael numbers.
Every composite number is a Knödel number. This can be seen by setting 
equal to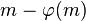 
.
Examples
| n | Kn | |
|---|---|---|
| 1 | {561, 1105, 1729, 2465, 2821, 6601, ... } | (sequence A002997 in OEIS) |
| 2 | {4, 6, 8, 10, 12, 14, 22, 24, 26, ... } | (sequence A050990 in OEIS) |
| 3 | {9, 15, 21, 33, 39, 51, 57, 63, 69, ... } | (sequence A033553 in OEIS) |
| 4 | {6, 8, 12, 16, 20, 24, 28, 40, 44, ... } | (sequence A050992 in OEIS) |
Literature
- Makowski, A (1963). Generalization of Morrow's D-Numbers. p. 71.
- Ribenboim, Paulo (1989). The New Book of Prime Number Records. New York: Springer-Verlag. p. 101. ISBN 978-0-387-94457-9.
- Weisstein, Eric W., "Knödel Numbers", MathWorld.
References
- ↑ Walter Knödel, born May 20th, 1926 in Vienna, earned a Ph.D. in number theory in 1948 (advisors: Edmund Hlawka and Johann Radon) and obtained the habilitation in 1953. Since 1961 he is professor at University of Stuttgart, establishing the new department of computer science. See also The web page on Walter Knödel at the University of Stuttgart.
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
This article is issued from Wikipedia - version of the Monday, October 26, 2015. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.