Kleinian integer
In mathematical cryptography, a Kleinian integer is a complex number of the form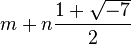 
, with m and n rational integers. They are named after Felix Klein.
The Kleinian integers form a ring called the Kleinian ring, which is the ring of integers in the imaginary quadratic field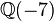 
. This ring is a unique factorization domain.
See also
References
- Conway, John Horton; Smith, Derek A. (2003), On Quaternions and Octonions: Their Geometry, Arithmetic, and Symmetry, A. K. Peters, Ltd., ISBN 1-56881-134-9. (Review).
- Dimitrov, V. S.; Järvinen, K. U.; Jacobson, M. J.; Chan, W. F.; Huang, Z. (2006), "FPGA Implementation of Point Multiplication on Koblitz Curves Using Kleinian Integers", Cryptographic Hardware and Embedded Systems - CHES 2006, Lecture Notes in Computer Science 4249, pp. 445–459, doi:10.1007/11894063_35, ISBN 978-3-540-46559-1
This article is issued from Wikipedia - version of the Tuesday, February 10, 2015. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.