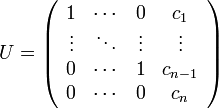Klein polyhedron

In the geometry of numbers, the Klein polyhedron, named after Felix Klein, is used to generalize the concept of continued fractions to higher dimensions.

Definition

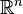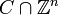Let $\textstyle C$ be a closed simplicial cone in Euclidean space $\textstyle \mathbb{R}^n$ . The Klein polyhedron of $\textstyle C$ is the convex hull of the non-zero points of $\textstyle C \cap \mathbb{Z}^n$ .

Relation to continued fractions

Suppose $\textstyle \alpha > 0$ is an irrational number. In 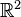$\textstyle \mathbb{R}^2$ , the cones generated by 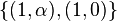$\textstyle \{(1, \alpha), (1, 0)\}$ and by 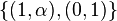$\textstyle \{(1, \alpha), (0, 1)\}$ give rise to two Klein polyhedra, each of which is bounded by a sequence of adjoining line segments. Define the integer length of a line segment to be one less than the size of its intersection with 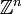$\textstyle \mathbb{Z}^n$ . Then the integer lengths of the edges of these two Klein polyhedra encode the continued-fraction expansion of $\textstyle \alpha$ , one matching the even terms and the other matching the odd terms.

Graphs associated with the Klein polyhedron

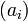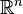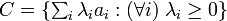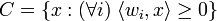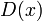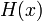Suppose $\textstyle C$ is generated by a basis $\textstyle (a_i)$ of $\textstyle \mathbb{R}^n$ (so that $\textstyle C = \{ \sum_i \lambda_i a_i : (\forall i) \; \lambda_i \geq 0 \}$ ), and let $\textstyle (w_i)$ be the dual basis (so that $\textstyle C = \{ x : (\forall i) \; \langle w_i, x \rangle \geq 0\}$ ). Write $\textstyle D(x)$ for the line generated by the vector $\textstyle x$ , and $\textstyle H(x)$ for the hyperplane orthogonal to $\textstyle x$ .

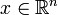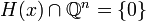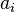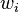Call the vector $\textstyle x \in \mathbb{R}^n$ irrational if $\textstyle H(x) \cap \mathbb{Q}^n = \{0\}$ ; and call the cone $\textstyle C$ irrational if all the vectors $\textstyle a_i$ and $\textstyle w_i$ are irrational.

The boundary $\textstyle V$ of a Klein polyhedron is called a sail. Associated with the sail $\textstyle V$ of an irrational cone are two graphs:

the graph $\textstyle \Gamma_{\mathrm e}(V)$ whose vertices are vertices of $\textstyle V$ , two vertices being joined if they are endpoints of a (one-dimensional) edge of $\textstyle V$ ;
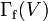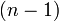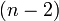the graph $\textstyle \Gamma_{\mathrm f}(V)$ whose vertices are $\textstyle (n-1)$ -dimensional faces (chambers) of $\textstyle V$ , two chambers being joined if they share an $\textstyle (n-2)$ -dimensional face.

Both of these graphs are structurally related to the directed graph 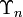$\textstyle \Upsilon_n$ whose set of vertices is 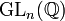$\textstyle \mathrm{GL}_n(\mathbb{Q})$ , where vertex 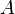$\textstyle A$ is joined to vertex 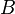$\textstyle B$ if and only if 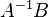$\textstyle A^{-1}B$ is of the form 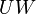$\textstyle UW$ where

U = \left( \begin{array}{cccc} 1 & \cdots & 0 & c_1 \\ \vdots & \ddots & \vdots & \vdots \\ 0 & \cdots & 1 & c_{n-1} \\ 0 & \cdots & 0 & c_n \end{array} \right)

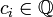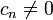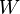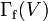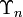(with $\textstyle c_i \in \mathbb{Q}$ , $\textstyle c_n \neq 0$ ) and $\textstyle W$ is a permutation matrix. Assuming that $\textstyle V$ has been triangulated, the vertices of each of the graphs $\textstyle \Gamma_{\mathrm e}(V)$ and $\textstyle \Gamma_{\mathrm f}(V)$ can be described in terms of the graph $\textstyle \Upsilon_n$ :

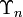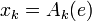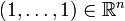Given any path $\textstyle (x_0, x_1, \ldots)$ in $\textstyle \Gamma_{\mathrm e}(V)$ , one can find a path $\textstyle (A_0, A_1, \ldots)$ in $\textstyle \Upsilon_n$ such that $\textstyle x_k = A_k (e)$ , where $\textstyle e$ is the vector $\textstyle (1, \ldots, 1) \in \mathbb{R}^n$ .
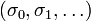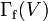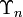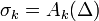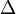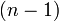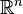Given any path $\textstyle (\sigma_0, \sigma_1, \ldots)$ in $\textstyle \Gamma_{\mathrm f}(V)$ , one can find a path $\textstyle (A_0, A_1, \ldots)$ in $\textstyle \Upsilon_n$ such that $\textstyle \sigma_k = A_k (\Delta)$ , where $\textstyle \Delta$ is the $\textstyle (n-1)$ -dimensional standard simplex in $\textstyle \mathbb{R}^n$ .

Generalization of Lagrange's theorem

Lagrange proved that for an irrational real number $\textstyle \alpha$ , the continued-fraction expansion of $\textstyle \alpha$ is periodic if and only if $\textstyle \alpha$ is a quadratic irrational. Klein polyhedra allow us to generalize this result.

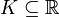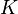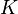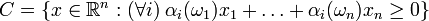Let $\textstyle K \subseteq \mathbb{R}$ be a totally real algebraic number field of degree $\textstyle n$ , and let $\textstyle \alpha_i : K \to \mathbb{R}$ be the $\textstyle n$ real embeddings of $\textstyle K$ . 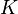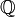The simplicial cone $\textstyle C$ is said to be split over $\textstyle K$ if $\textstyle C = \{ x \in \mathbb{R}^n : (\forall i) \; \alpha_i(\omega_1) x_1 + \ldots + \alpha_i(\omega_n) x_n \geq 0 \}$ where $\textstyle \omega_1, \ldots, \omega_n$ is a basis for $\textstyle K$ over $\textstyle \mathbb{Q}$ .

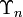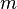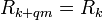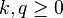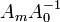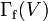Given a path $\textstyle (A_0, A_1, \ldots)$ in $\textstyle \Upsilon_n$ , let $\textstyle R_k = A_{k+1} A_k^{-1}$ . The path is called periodic, with period $\textstyle m$ , if $\textstyle R_{k+qm} = R_k$ for all $\textstyle k, q \geq 0$ . The period matrix of such a path is defined to be $\textstyle A_m A_0^{-1}$ . A path in $\textstyle \Gamma_{\mathrm e}(V)$ or $\textstyle \Gamma_{\mathrm f}(V)$ associated with such a path is also said to be periodic, with the same period matrix.

The generalized Lagrange theorem states that for an irrational simplicial cone 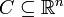$\textstyle C \subseteq \mathbb{R}^n$ , with generators 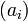$\textstyle (a_i)$ and $\textstyle (w_i)$ as above and with sail $\textstyle V$ , the following three conditions are equivalent:

$\textstyle C$ is split over some totally real algebraic number field of degree $\textstyle n$ .
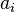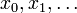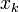For each of the $\textstyle a_i$ there is periodic path of vertices $\textstyle x_0, x_1, \ldots$ in $\textstyle \Gamma_{\mathrm e}(V)$ such that the $\textstyle x_k$ asymptotically approach the line 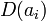$\textstyle D(a_i)$ ; and the period matrices of these paths all commute.
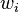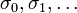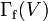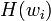For each of the $\textstyle w_i$ there is periodic path of chambers $\textstyle \sigma_0, \sigma_1, \ldots$ in $\textstyle \Gamma_{\mathrm f}(V)$ such that the $\textstyle \sigma_k$ asymptotically approach the hyperplane $\textstyle H(w_i)$ ; and the period matrices of these paths all commute.

Example

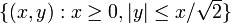Take $\textstyle n = 2$ and $\textstyle K = \mathbb{Q}(\sqrt{2})$ . Then the simplicial cone $\textstyle \{(x,y) : x \geq 0, \vert y \vert \leq x / \sqrt{2}\}$ is split over 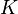$\textstyle K$ . The vertices of the sail are the points 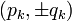$\textstyle (p_k, \pm q_k)$ corresponding to the even convergents 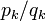$\textstyle p_k / q_k$ of the continued fraction for 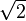$\textstyle \sqrt{2}$ . 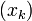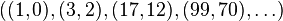The path of vertices $\textstyle (x_k)$ in the positive quadrant starting at $\textstyle (1, 0)$ and proceeding in a positive direction is $\textstyle ((1,0), (3,2), (17,12), (99,70), \ldots)$ . 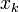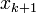Let $\textstyle \sigma_k$ be the line segment joining $\textstyle x_k$ to $\textstyle x_{k+1}$ . 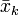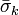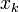Write $\textstyle \bar{x}_k$ and $\textstyle \bar{\sigma}_k$ for the reflections of $\textstyle x_k$ and $\textstyle \sigma_k$ in the $\textstyle x$ -axis. 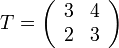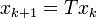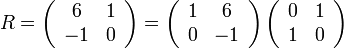Let $\textstyle T = \left( \begin{array}{cc} 3 & 4 \\ 2 & 3 \end{array} \right)$ , so that $\textstyle x_{k+1} = T x_k$ , and let $\textstyle R = \left( \begin{array}{cc} 6 & 1 \\ -1 & 0 \end{array} \right) = \left( \begin{array}{cc} 1 & 6 \\ 0 & -1 \end{array} \right) \left( \begin{array}{cc} 0 & 1 \\ 1 & 0 \end{array} \right)$ .

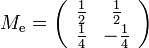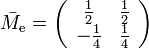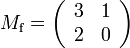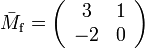Let $\textstyle M_{\mathrm e} = \left( \begin{array}{cc} \frac12 & \frac12 \\ \frac14 & -\frac14 \end{array} \right)$ , $\textstyle \bar{M}_{\mathrm e} = \left( \begin{array}{cc} \frac12 & \frac12 \\ -\frac14 & \frac14 \end{array} \right)$ , $\textstyle M_{\mathrm f} = \left( \begin{array}{cc} 3 & 1 \\ 2 & 0 \end{array} \right)$ , and $\textstyle \bar{M}_{\mathrm f} = \left( \begin{array}{cc} 3 & 1 \\ -2 & 0 \end{array} \right)$ .

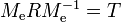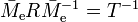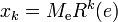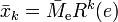The paths $\textstyle (M_{\mathrm e} R^k)$ and $\textstyle (\bar{M}_{\mathrm e} R^k)$ are periodic (with period one) in $\textstyle \Upsilon_2$ , with period matrices $\textstyle M_{\mathrm e} R M_{\mathrm e}^{-1} = T$ and $\textstyle \bar{M}_{\mathrm e} R \bar{M}_{\mathrm e}^{-1} = T^{-1}$ . We have $\textstyle x_k = M_{\mathrm e} R^k (e)$ and $\textstyle \bar{x}_k = \bar{M}_{\mathrm e} R^k (e)$ .
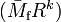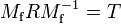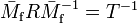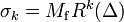The paths $\textstyle (M_{\mathrm f} R^k)$ and $\textstyle (\bar{M}_{\mathrm f} R^k)$ are periodic (with period one) in $\textstyle \Upsilon_2$ , with period matrices $\textstyle M_{\mathrm f} R M_{\mathrm f}^{-1} = T$ and $\textstyle \bar{M}_{\mathrm f} R \bar{M}_{\mathrm f}^{-1} = T^{-1}$ . We have $\textstyle \sigma_k = M_{\mathrm f} R^k (\Delta)$ and $\textstyle \bar{\sigma}_k = \bar{M}_{\mathrm f} R^k (\Delta)$ .

Generalization of approximability

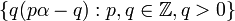A real number $\textstyle \alpha > 0$ is called badly approximable if $\textstyle \{ q (p \alpha - q) : p,q \in \mathbb{Z}, q > 0\}$ is bounded away from zero. An irrational number is badly approximable if and only if the partial quotients of its continued fraction are bounded.^[1] This fact admits of a generalization in terms of Klein polyhedra.

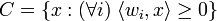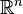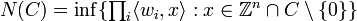Given a simplicial cone $\textstyle C = \{ x : (\forall i) \; \langle w_i, x \rangle \geq 0\}$ in $\textstyle \mathbb{R}^n$ , where $\textstyle \langle w_i, w_i \rangle = 1$ , define the norm minimum of $\textstyle C$ as $\textstyle N(C) = \inf \{ \prod_i \langle w_i, x \rangle : x \in \mathbb{Z}^n \cap C \setminus \{0\} \}$ .

Given vectors $\textstyle \mathbf{v}_1, \ldots, \mathbf{v}_m \in \mathbb{Z}^n$ , let $\textstyle [\mathbf{v}_1, \ldots, \mathbf{v}_m] = \sum_{i_1 < \cdots < i_n} \vert \det(\mathbf{v}_{i_1} \cdots \mathbf{v}_{i_n}) \vert$ . This is the Euclidean volume of $\textstyle \{ \sum_i \lambda_i \mathbf{v}_i : (\forall i) \; 0 \leq \lambda_i \leq 1 \}$ .

Let $\textstyle V$ be the sail of an irrational simplicial cone $\textstyle C$ .

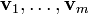For a vertex $\textstyle x$ of $\textstyle \Gamma_{\mathrm e}(V)$ , define $\textstyle [x] = [\mathbf{v}_1, \ldots, \mathbf{v}_m]$ where $\textstyle \mathbf{v}_1, \ldots, \mathbf{v}_m$ are primitive vectors in 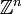$\textstyle \mathbb{Z}^n$ generating the edges emanating from $\textstyle x$ .
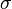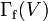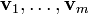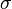For a vertex $\textstyle \sigma$ of $\textstyle \Gamma_{\mathrm f}(V)$ , define $\textstyle [\sigma] = [\mathbf{v}_1, \ldots, \mathbf{v}_m]$ where $\textstyle \mathbf{v}_1, \ldots, \mathbf{v}_m$ are the extreme points of $\textstyle \sigma$ .

Then 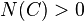$\textstyle N(C) > 0$ if and only if $\textstyle \{ [x] : x \in \Gamma_{\mathrm e}(V) \}$ and $\textstyle \{ [\sigma] : \sigma \in \Gamma_{\mathrm f}(V) \}$ are both bounded.

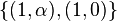The quantities $\textstyle [x]$ and $\textstyle [\sigma]$ are called determinants. In two dimensions, with the cone generated by $\textstyle \{(1, \alpha), (1,0)\}$ , they are just the partial quotients of the continued fraction of $\textstyle \alpha$ .

References

↑ Bugeaud, Yann (2012). Distribution modulo one and Diophantine approximation. Cambridge Tracts in Mathematics 193. Cambridge: Cambridge University Press. p. 245. ISBN 978-0-521-11169-0. Zbl pre06066616.

O. N. German, 2007, "Klein polyhedra and lattices with positive norm minima". Journal de théorie des nombres de Bordeaux 19: 175–190.
E. I. Korkina, 1995, "Two-dimensional continued fractions. The simplest examples". Proc. Steklov Institute of Mathematics 209: 124–144.
G. Lachaud, 1998, "Sails and Klein polyhedra" in Contemporary Mathematics 210. American Mathematical Society: 373–385.

This article is issued from Wikipedia - version of the Sunday, January 31, 2016. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.