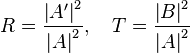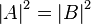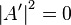Klein paradox
In 1929, physicist Oskar Klein[1] obtained a surprising result by applying the Dirac equation to the familiar problem of electron scattering from a potential barrier. In nonrelativistic quantum mechanics, electron tunneling into a barrier is observed, with exponential damping. However, Klein’s result showed that if the potential is of the order of the electron mass, 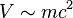 , the barrier is nearly transparent. Moreover, as the potential approaches infinity, the reflection diminishes and the electron is always transmitted.
, the barrier is nearly transparent. Moreover, as the potential approaches infinity, the reflection diminishes and the electron is always transmitted.
The immediate application of the paradox was to Rutherford's proton–electron model for neutral particles within the nucleus, before the discovery of the neutron. The paradox presented a quantum mechanical objection to the notion of an electron confined within a nucleus.[2] This clear and precise paradox suggested that an electron could not be confined within a nucleus by any potential well. The meaning of this paradox was intensely debated at the time.[2]
Massless particles
Consider a massless relativistic particle approaching a potential step of height 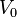 with energy
with energy 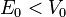 and momentum
and momentum  .
.

The particle's wave function, 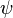 , follows the time-independent Dirac equation:
, follows the time-independent Dirac equation:
And 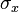 is the Pauli matrix:
is the Pauli matrix:

Assuming the particle is propagating from the left, we obtain two solutions — one before the step, in region (1) and one under the potential, in region (2):
Where the coefficients A, A′ and B are complex numbers. Both the incoming and transmitted wave functions are associated with positive group velocity (Blue lines in Fig.1), whereas the reflected wave function is associated with negative group velocity. (Green lines in Fig.1)
We now want to calculate the transmission and reflection coefficients, 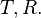 They are derived from the probability amplitude currents.
They are derived from the probability amplitude currents.
The definition of the probability current associated with the Dirac equation is:
In this case:
The transmission and reflection coefficients are:
Continuity of the wave function at 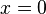 , yields:
, yields:
And so the transmission coefficient is 1 and there is no reflection.
One interpretation of the paradox is that a potential step cannot reverse the direction of the group velocity of a massless relativistic particle. This explanation best suits the single particle solution cited above. Other, more complex interpretations are suggested in literature, in the context of quantum field theory where the unrestrained tunnelling is shown to occur due to the existence of particle–antiparticle pairs at the potential.
Massive case
For the massive case, the calculations are similar to the above. The results are as surprising as in the massless case. The transmission coefficient is always larger than zero, and approaches 1 as the potential step goes to infinity.
The Klein zone
If the energy of the particle is in the range 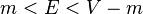 , then partial reflection rather than total reflection will result.
, then partial reflection rather than total reflection will result.
Resolutions for the massive case
While the traditional resolution uses particle/anti-particle pair production in the context of quantum field theory (Hansen 1981), a simpler resolution exists that substitutes physical pair production for the scattering of negative energy solutions under the barrier (Alhaidari 2009). This strategy was also applied to obtain analytic solutions to the Dirac equation for an infinite square well.
Other cases
These results were expanded to higher dimensions, and to other types of potentials, such as a linear step, a square barrier, etc. Many experiments in electron transport in graphene rely on the Klein paradox for massless particles.[3][4]
See also
References
- ↑ Klein, O. (1929). "Die Reflexion von Elektronen an einem Potentialsprung nach der relativistischen Dynamik von Dirac". Zeitschrift für Physik 53 (3–4): 157. Bibcode:1929ZPhy...53..157K. doi:10.1007/BF01339716.
- 1 2 Stuewer, Roger H. (1985). "Niels Bohr and Nuclear Physics". In French, A. P.; Kennedy, P. J. Niels Bohr: A Centenary Volume. Harvard University Press. pp. 197–220. ISBN 0674624165.
- ↑ Katsnelson, M. I.; Novoselov, K. S.; Geim, A. K. (2006). "Chiral tunnelling and the Klein paradox in graphene". Nature Physics 2 (9): 620. arXiv:cond-mat/0604323. Bibcode:2006NatPh...2..620K. doi:10.1038/nphys384.
- ↑ Pendry, J. B. (2007). "PHYSICS: Negative Refraction for Electrons?". Science 315 (5816): 1226–7. doi:10.1126/science.1140178. PMID 17332397.
Further reading
- Dombey, N; Calogeracos, A. (July 1999). "Seventy years of the Klein paradox". Physics Reports 315 (1–3): 41–58. Bibcode:1999PhR...315...41D. doi:10.1016/S0370-1573(99)00023-X.
- Robinson, T. R. (2012). "On Klein tunneling in graphene". American Journal of Physics 80 (2): 141–147. Bibcode:2012AmJPh..80..141R. doi:10.1119/1.3658629.
- Calogeracos, A.; Dombey, N. (1999). "History and physics of the Klein paradox". Contemporary Physics 40 (5): 313. arXiv:quant-ph/9905076. Bibcode:1999ConPh..40..313C. doi:10.1080/001075199181387.
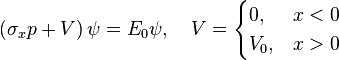
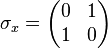
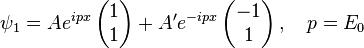
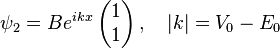
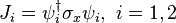
![J_1=2\left[\left| A \right|^2-\left| A' \right|^2\right], \quad J_2=2\left| B \right|^2 \,](../I/m/abce0c1b8dd4fdb461a8fe64da23eaef.png)