Kirkman's schoolgirl problem

Original publication of the problem

Kirkman's schoolgirl problem is a problem in combinatorics proposed by Rev. Thomas Penyngton Kirkman in 1850 as Query VI in The Lady's and Gentleman's Diary (pg.48). The problem states:

Fifteen young ladies in a school walk out three abreast for seven days in succession: it is required to arrange them daily so that no two shall walk twice abreast.[1]

Solution

If the girls are numbered from 01 to 15, the following arrangement is one solution:[2]

Sun. Mon. Tues. Wed. Thurs. Fri. Sat.
01, 06, 11 01, 02, 05 02, 03, 06 05, 06, 09 03, 05, 11 05, 07, 13 11, 13, 04
02, 07, 12 03, 04, 07 04, 05, 08 07, 08, 11 04, 06, 12 06, 08, 14 12, 14, 05
03, 08, 13 08, 09, 12 09, 10, 13 12, 13, 01 07, 09, 15 09, 11, 02 15, 02, 08
04, 09, 14 10, 11, 14 11, 12, 15 14, 15, 03 08, 10, 01 10, 12, 03 01, 03, 09
05, 10, 15 13, 15, 06 14, 01, 07 02, 04, 10 13, 14, 02 15, 01, 04 06, 07, 10

A solution to this problem is an example of a Kirkman triple system,[3] which is a Steiner triple system having a parallelism, that is, a partition of the blocks of the triple system into parallel classes which are themselves partitions of the points into disjoint blocks.

There are seven non-isomorphic solutions to the schoolgirl problem.[4] Two of these are packings of the finite projective space PG(3,2).[5] A packing of a projective space is a partition of the lines of the space into spreads, and a spread is a partition of the points of the space into lines. These "packing" solutions can be visualized as relations between a tetrahedron and its vertices, edges, and faces.[6]

A square, rather than tetrahedral, model may also be used:

The square model of PG(3,2)

For the origin of the square model, see the Cullinane diamond theorem.

History

The first solution was published by Arthur Cayley.[7] This was shortly followed by Kirkman's own solution[8] which was given as a special case of his considerations on combinatorial arrangements published three years prior.[9] J. J. Sylvester also investigated the problem and ended up declaring that Kirkman stole the idea from him. The puzzle appeared in several recreational mathematics books at the turn of the century by Lucas,[10] Rouse Ball,[11] Ahrens,[12] and Dudeney.[13]

Kirkman often complained about the fact that his substantial paper (Kirkman 1847) was totally eclipsed by the popular interest in the schoolgirl problem.[14]

Generalization

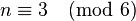The problem can be generalized to n girls, where n must be an odd multiple of 3 (that is n \equiv 3 \pmod{6}), walking in triplets for 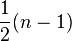\frac{1}{2}(n-1) days, with the requirement, again, that no pair of girls walk in the same row twice. The solution to this generalisation is a Steiner triple system, an S(2, 3, 6t + 3) with parallelism (that is, one in which each of the 6t + 3 elements occurs exactly once in each block of 3-element sets), known as a Kirkman triple system.[2] It is this generalization of the problem that Kirkman discussed first, while the famous special case 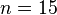n=15 was only proposed later.[9] A complete solution to the general case was published by D. K. Ray-Chaudhuri and R. M. Wilson in 1968,[15] though it had already been solved by Lu Jiaxi (陆家羲) in 1965,[16] but had not been published at that time.[17]

Many variations of the basic problem can be considered. Alan Hartman solves a problem of this type with the requirement that no trio walks in a row of four more than once[18] using Steiner quadruple systems.

More recently a similar problem known as the Social Golfer Problem has gained interest that deals with 20 golfers who want to get to play with different people each day in groups of 4.

As this is a regrouping strategy where all groups are orthogonal, this process within the problem of organising a large group into smaller groups where no two people share the same group twice can be referred to as orthogonal regrouping. However, this term is currently not commonly used and evidence suggests that there isn't a common name for the process.

Other applications

Notes

  1. ↑ (Graham, Grötschel & Lovász 1995)
  2. 1 2 (Ball & Coxeter 1974)
  3. ↑ Weisstein, Eric W., "Kirkman's Schoolgirl Problem", MathWorld.
  4. ↑ (Cole 1922)
  5. ↑ (Hirschfeld 1985, pg.75)
  6. ↑ Falcone & Pavone 2011
  7. ↑ Cayley 1850
  8. ↑ Kirkman 1850
  9. 1 2 Kirkman 1847
  10. ↑ Lucas 1883
  11. ↑ Rouse Ball 1892
  12. ↑ Ahrens 1901
  13. ↑ Dudeney 1917
  14. ↑ Cummings 1918
  15. ↑ Ray-Chaudhuri & Wilson 1971
  16. ↑ Jiaxi 1990
  17. ↑ Colbourn & Dinitz 2007, p. 13
  18. ↑ (Hartman 1980)

References

This article is issued from Wikipedia - version of the Sunday, January 31, 2016. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.