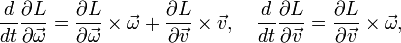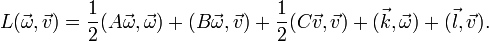Kirchhoff equations
In fluid dynamics, the Kirchhoff equations, named after Gustav Kirchhoff, describe the motion of a rigid body in an ideal fluid.
where 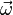 and
and 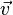 are the angular and linear velocity vectors at the point
are the angular and linear velocity vectors at the point 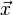 , respectively;
, respectively;  is the moment of inertia tensor,
is the moment of inertia tensor,  is the body's mass;
is the body's mass;  is
a unit normal to the surface of the body at the point
is
a unit normal to the surface of the body at the point 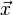 ;
;
 is a pressure at this point;
is a pressure at this point; 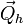 and
and 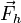 are the hydrodynamic
torque and force acting on the body, respectively;
are the hydrodynamic
torque and force acting on the body, respectively;
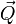 and
and  likewise denote all other torques and forces acting on the
body. The integration is performed over the fluid-exposed portion of the
body's surface.
likewise denote all other torques and forces acting on the
body. The integration is performed over the fluid-exposed portion of the
body's surface.
If the body is completely submerged body in an infinitely large volume of irrotational, incompressible, inviscid fluid, that is at rest at infinity, then the vectors 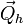 and
and 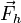 can be found via explicit integration, and the dynamics of the body is described by the Kirchhoff – Clebsch equations:
can be found via explicit integration, and the dynamics of the body is described by the Kirchhoff – Clebsch equations:
Their first integrals read
-
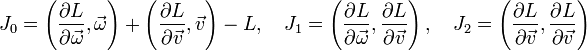 .
.
Further integration produces explicit expressions for position and velocities.
References
- Kirchhoff G. R. Vorlesungen ueber Mathematische Physik, Mechanik. Lecture 19. Leipzig: Teubner. 1877.
- Lamb, H., Hydrodynamics. Sixth Edition Cambridge (UK): Cambridge University Press. 1932.
![\begin{align}
{d\over{dt}} {{\partial T}\over{\partial \vec \omega}}
& = {{\partial T}\over{\partial \vec \omega}} \times \vec \omega + {{\partial
T}\over{\partial \vec v}} \times \vec v + \vec Q_h + \vec Q, \\[10pt]
{d\over{dt}} {{\partial T}\over{\partial \vec v}}
& = {{\partial T}\over{\partial \vec v}} \times \vec \omega + \vec F_h + \vec F, \\[10pt]
T & = {1 \over 2} \left( \vec \omega^T \tilde I \vec \omega + m v^2 \right) \\[10pt]
\vec Q_h & =-\int p \vec x \times \hat n \, d\sigma, \\[10pt]
\vec F_h & =-\int p \hat n \, d\sigma
\end{align}](../I/m/ea760e3b133895e17844c25af171a93b.png)