Kinetic proofreading

Kinetic proofreading (or kinetic amplification) is a mechanism for error correction in biochemical reactions, proposed independently by John Hopfield (1974) and Jacques Ninio (1975). Kinetic proofreading allows enzymes to discriminate between two possible reaction pathways leading to correct or incorrect products with an accuracy higher than what one would predict based on the difference in the activation energy between these two pathways.^[1]^[2]

Increased specificity is obtained by introducing an irreversible step exiting the pathway, with reaction intermediates leading to incorrect products more likely to prematurely exit the pathway than reaction intermediates leading to the correct product. If the exit step is fast relative to the next step in the pathway, the specificity can be increased by a factor of up to the ratio between the two exit rate constants. (If the next step is fast relative to the exit step, specificity will not be increased because there will not be enough time for exit to occur.) This can be repeated more than once to increase specificity further.

Specificity paradox

In protein synthesis, the error rate is on the order of 1 in 10,000. This means that when a ribosome is matching anticodons of tRNA to the codons of mRNA, it matches complementary sequences correctly nearly all the time. Hopfield noted that because of how similar the substrates are (the difference between a wrong codon and a right codon can be as small as a difference in a single base), an error rate that small is unachievable with a one-step mechanism. Both wrong and right tRNA can bind to the ribosome, and if the ribosome can only discriminate between them by complementary matching of the anticodon, it must rely on the small free energy difference between binding three matched complementary bases or only two.

A one-shot machine which tests whether the codons match or not by examining whether the codon and anticodon are bound will not be able to tell the difference between wrong and right codon with an error rate less than 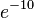$e^{-10}$ unless the free energy difference is at least 10kT, which is much larger than the free energy difference for single codon binding. This is a thermodynamic bound, so it cannot be evaded by building a different machine. However, this can be overcome by kinetic proofreading, which introduces an irreversible step through the input of energy.^[3]

Another molecular recognition mechanism, which does not require expenditure of free energy is that of conformational proofreading. The incorrect product may also be formed but hydrolyzed at a greater rate than the correct product, giving the possibility of theoretically infinite specificity the longer you let this reaction run, but at the cost of large amounts of the correct product as well. (Thus there is a tradeoff between product production and its efficiency.) The hydrolytic activity may be on the same enzyme, as in DNA polymerases with editing functions, or on different enzymes.

Multistep ratchet

Hopfield suggested a simple way to achieve smaller error rates using a molecular ratchet which takes many irreversible steps, each testing to see if the sequences match. At each step, energy is expended and specificity (the ratio of correct substrate to incorrect substrate at that point in the pathway) increases.

The requirement for energy in each step of the ratchet is due to the need for the steps to be irreversible; for specificity to increase, entry of substrate and analogue must occur largely through the entry pathway, and exit largely through the exit pathway. If entry were an equilibrium, the earlier steps would form a pre-equilibrium and the specificity benefits of entry into the pathway (less likely for the substrate analogue) would be lost; if the exit step were an equilibrium, then the substrate analogue would be able to re-enter the pathway through the exit step, bypassing the specificity of earlier steps altogether.

Although one test will only be able to discriminate between mismatched and matched sequences a fraction 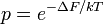$p=e^{-\Delta F/kT}$ of the time, two tests will both fail only $p^2$ of the time, and N tests will fail $p^N$ of the time. In terms of free energy, the discrimination power of N successive tests for two states with a free energy $\Delta F$ is the same as one test between two states with a free energy $N\Delta F$ .

To achieve an error rate of 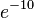$e^{-10}$ requires several comparison steps. Hopfield predicted on the basis of this theory that there is a multistage ratchet in the ribosome which tests the match several times before incorporating the next amino acid into the protein.

Experimental examples

Charging tRNAs with their respective amino-acids – the enzyme that charges the tRNA is called aminoacyl tRNA synthetase. This enzyme utilizes a high energy intermediate state to increase the fidelity of binding the right pair of tRNA and amino-acid.^[4] In this case, energy is used to make the high-energy intermediate (making the entry pathway irreversible), and the exit pathway is irreversible by virtue of the high energy difference in dissociation.

Homologous recombination – Homologous recombination facilitates the exchange between homologous or almost homologous DNA strands. During this process, the RecA protein polymerizes along a DNA and this DNA-protein filament searches for a homologous DNA sequence. Both processes of RecA polymerization^[5]^[6] and homology search^[7] utilize the kinetic proofreading mechanism.

DNA damage recognition and repair – a certain DNA repair mechanism utilizes kinetic proofreading to discriminate damaged DNA.^[8] Some DNA polymerases can also detect when they have added an incorrect base and are able to hydrolyze it immediately; in this case, the irreversible (energy-requiring) step is addition of the base.

Theoretical considerations

Universal first passage time

Biochemical processes that use kinetic proofreading to improve specificity implement the delay-inducing multistep ratchet by a variety of distinct biochemical networks. Nonetheless, many such networks result in the times to completion of the molecular assembly and the proofreading steps (also known as the first passage time) that approach a near-universal, exponential shape for high proofreading rates and large network sizes.^[9] Since exponential completion times are characteristic of a two-state Markov process, this observation makes kinetic proofreading one of only a few examples of biochemical processes where structural complexity results in a much simpler large-scale, phenomenological dynamics.

Topology of kinetic proofreading

The increase in specificity, or the overall amplification factor of a kinetic proofreading network that may include multiple pathways and especially loops is intimately related to the topology of the network: the specificity grows exponentially with the number of loops in the network.^[10]^[11] An example is homologous recombination in which the number of loops scales like the square of DNA length.^[5]^[6] The universal completion time emerges precisely in this regime of large number of loops and high amplification.^[10]

References

↑ JJ Hopfield (October 1974). "Kinetic proofreading: a new mechanism for reducing errors in biosynthetic processes requiring high specificity". Proc. Natl. Acad. Sci. U.S.A. 71 (10): 4135–9. Bibcode:1974PNAS...71.4135H. doi:10.1073/pnas.71.10.4135. PMC 434344. PMID 4530290.
↑ Ninio J (1975). "Kinetic amplification of enzyme discrimination". Biochimie 57 (5): 587–95. doi:10.1016/S0300-9084(75)80139-8. PMID 1182215.
↑ Guéron M (1978). "Enhanced selectivity of enzymes by kinetic proofreading". Am. Sci. 66 (2): 202–8. Bibcode:1978AmSci..66..202G. PMID 646212.
↑ Hopfield JJ, Yamane T, Yue V, Coutts SM (April 1976). "Direct experimental evidence for kinetic proofreading in amino acylation of tRNAIle". Proc. Natl. Acad. Sci. U.S.A. 73 (4): 1164–8. Bibcode:1976PNAS...73.1164H. doi:10.1073/pnas.73.4.1164. PMC 430221. PMID 1063397.
1 2 Bar-Ziv R, Tlusty T, Libchaber A (September 2002). "Protein-DNA computation by stochastic assembly cascade". Proc. Natl. Acad. Sci. U.S.A. 99 (18): 11589–92. arXiv:1008.0737. Bibcode:2002PNAS...9911589B. doi:10.1073/pnas.162369099. PMC 129313. PMID 12186973.
1 2 Tlusty T, Bar-Ziv R, Libchaber A (December 2004). "High-fidelity DNA sensing by protein binding fluctuations". Phys. Rev. Lett. 93 (25): 258103. arXiv:1008.0743. Bibcode:2004PhRvL..93y8103T. doi:10.1103/PhysRevLett.93.258103. PMID 15697950.
↑ Sagi D, Tlusty T, Stavans J (2006). "High fidelity of RecA-catalyzed recombination: a watchdog of genetic diversity". Nucleic Acids Res. 34 (18): 5021–31. doi:10.1093/nar/gkl586. PMC 1636419. PMID 16990254.
↑ Reardon JT, Sancar A (February 2004). "Thermodynamic cooperativity and kinetic proofreading in DNA damage recognition and repair". Cell Cycle 3 (2): 141–4. doi:10.4161/cc.3.2.645. PMID 14712076.
↑ Bel G, Munsky B, Nemenman I (March 2010). "The simplicity of completion time distributions for common complex biochemical processes". Phys Biol 7 (1): 016003. arXiv:0904.1587. Bibcode:2010PhBio...7a6003B. doi:10.1088/1478-3975/7/1/016003. PMID 20026876.
1 2 B Munsky, I Nemenman and G Bel (Dec 2009). "Specificity and completion time distributions of biochemical processes". J. Chem. Phys. 131 (23): 235103. doi:10.1063/1.3274803. PMID 20025351.
↑ A Murugan, D Huse and S Leibler (July 2012). "Speed, dissipation, and error in kinetic proofreading". Proc. Natl. Acad. Sci. U.S.A. 109 (30): 12034–9. Bibcode:2012PNAS..10912034M. doi:10.1073/pnas.1119911109. PMC 3409783. PMID 22786930.