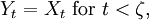Killed process
For killed processes in computer operating systems, see Process state#Terminated.
In probability theory — specifically, in stochastic analysis — a killed process is a stochastic process that is forced to assume an undefined or "killed" state at some (possibly random) time.
Definition
Let X : T × Ω → S be a stochastic process defined for "times" t in some ordered index set T, on a probability space (Ω, Σ, P), and taking values in a measurable space S. Let ζ : Ω → T be a random time, referred to as the killing time. Then the killed process Y associated to X is defined by
and Yt is left undefined for t ≥ ζ. Alternatively, one may set Yt = c for t ≥ ζ, where c is a "coffin state" not in S.
See also
References
- Øksendal, Bernt K. (2003). Stochastic Differential Equations: An Introduction with Applications (Sixth ed.). Berlin: Springer. ISBN 3-540-04758-1. (See Section 8.2)
This article is issued from Wikipedia - version of the Wednesday, August 05, 2015. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.