KdV hierarchy
In mathematics, the KdV hierarchy is an infinite sequence of partial differential equations which starts with the Korteweg–de Vries equation.
Let  be translation operator defined on real valued functions as
be translation operator defined on real valued functions as 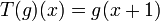 . Let
. Let  be set of all analytic functions that satisfy
be set of all analytic functions that satisfy 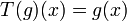 , i.e. periodic functions of period 1. For each
, i.e. periodic functions of period 1. For each 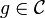 , define an operator
, define an operator
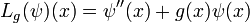 on the space of smooth functions on
on the space of smooth functions on 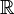 . We define the Bloch spectrum
. We define the Bloch spectrum 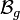 to be the set of
to be the set of 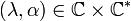 such that there is a nonzero function
such that there is a nonzero function 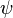 with
with 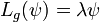 and
and 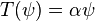 . The KdV hierarchy is a sequence of nonlinear differential operators
. The KdV hierarchy is a sequence of nonlinear differential operators 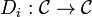 such that for any
such that for any  we have an analytic function
we have an analytic function 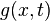 and we define
and we define 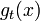 to be
to be 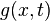 and
and
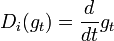 ,
then
,
then 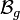 is independent of
is independent of  .
.
The KdV hierarchy arises naturally as a statement of Huygens' principle for the D'Alembertian.[1][2]
See also
References
- ↑ Fabio A. C. C. Chalub1 and Jorge P. Zubelli, "Huygens’ Principle for Hyperbolic Operators and Integrable Hierarchies"
- ↑ Yuri Yu. Berest and Igor M. Loutsenko, "Huygens’ Principle in Minkowski Spaces and Soliton Solutions of the Korteweg-de Vries Equation", arXiv:solv-int/9704012 DOI 10.1007/s002200050235
- Gesztesy, Fritz; Holden, Helge (2003), Soliton equations and their algebro-geometric solutions. Vol. I, Cambridge Studies in Advanced Mathematics 79, Cambridge University Press, ISBN 978-0-521-75307-4, MR 1992536
External links
This article is issued from Wikipedia - version of the Sunday, January 17, 2016. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.