Kazimierz Zarankiewicz
Kazimierz Zarankiewicz (2 May 1902 – 5 September 1959) was a Polish mathematician, interested primarily in topology.
Biography
Zarankiewicz was born in Częstochowa. He studied at the University of Warsaw, together with Zygmunt Janiszewski, Stefan Mazurkiewicz, Wacław Sierpiński, Kazimierz Kuratowski, and Stanisław Saks.
During World War II, Zarankiewicz took part in illegal teaching, forbidden by the German authorities, and eventually was sent to a concentration camp. He successfully survived and became a teacher at Warsaw University of Technology.
He visited universities in Tomsk, Harvard, London, Vienna. He served as president of the Warsaw section of the Polish Mathematical Society and the International Astronautical Federation.
Research contributions
Zarankiewicz wrote works on cut-points in connected spaces, on conformal mappings, on complex functions and number theory, and triangular numbers.
The Zarankiewicz problem is named after Zarankiewicz. This problem asks, for a given size of (0,1)-matrix, how many matrix entries must be set equal to 1 in order to guarantee that the matrix contains at least one a × b submatrix is made up only of 1's. An equivalent formulation in extremal graph theory asks for the maximum number of edges in a bipartite graph with no complete bipartite subgraph Ka,b.
The Zarankiewicz crossing number conjecture in the mathematical field of graph theory is also named after Zarankiewicz. The conjecture states that the crossing number of a complete bipartite graph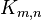 
equals
Zarankiewicz proved that this formula is an upper bound for the actual crossing number. The problem of determining the number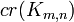 
was suggested by Paul Turán and became known as Turán's brick factory problem.
External links
- O'Connor, John J.; Robertson, Edmund F., "Kazimierz Zarankiewicz", MacTutor History of Mathematics archive, University of St Andrews.
- Zarankiewicz Crossing Number Conjecture at MathWorld
|