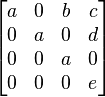Kasch ring

In ring theory, a subfield of abstract algebra, a right Kasch ring is a ring R for which every simple right R module is isomorphic to a right ideal of R.^[1] Analogously the notion of a left Kasch ring is defined, and the two notions are independent of each other.

Kasch rings are named in honor of mathematician Friedrich Kasch. Kasch originally called Artinian rings whose proper ideals have nonzero annihilators S-rings. (Kasch 1954)(Morita 1966) The characterizations below show that Kasch rings generalize S-rings.

Definition

Equivalent definitions will be introduced only for the right-hand version, with the understanding that the left-hand analogues are also true. The Kasch conditions have a few equivalences using the concept of annihilators, and this article uses the same notation appearing in the annihilator article.

In addition to the definition given in the introduction, the following properties are equivalent definitions for a ring R to be right Kasch. They appear in (Lam 1999, p. 281):

For every simple right R module S, there is a nonzero module homomorphism from M into R.
The maximal right ideals of R are right annihilators of ring elements, that is, each one is of the form 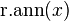$\mathrm{r.ann}(x)\,$ where x is in R.
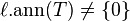For any maximal right ideal T of R, $\mathrm{\ell.ann}(T)\neq\{0\}$ .
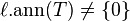For any proper right ideal T of R, $\mathrm{\ell.ann}(T)\neq\{0\}$ .
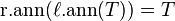For any maximal right ideal T of R, $\mathrm{r.ann}(\mathrm{\ell.ann}(T))=T$ .
R has no dense right ideals except R itself.

Examples

The content below can be found in references such as (Faith 1999, p. 109), (Lam 1999, §§8C,19B), (Nicholson & Yousif 2003, p.51).

Let R be a semiprimary ring with Jacobson radical J. If R is commutative, or if R/J is a simple ring, then R is right (and left) Kasch. In particular, commutative Artinian rings are right and left Kasch.

For a division ring k, consider a certain subring R of the four-by-four matrix ring with entries from k. The subring R consists of matrices of the following form:

\begin{bmatrix} a & 0 & b & c \\ 0 & a & 0 & d \\ 0 & 0 & a & 0 \\ 0 & 0 & 0 & e \end{bmatrix}

This is a right and left Artinian ring which is right Kasch, but not left Kasch.

Let S be the ring of power series on two noncommuting variables X and Y with coefficients from a field F. Let the ideal A be the ideal generated by the two elements YX and Y². The quotient ring S/A is a local ring which is right Kasch but not left Kasch.
Suppose R is a ring direct product of infinitely many nonzero rings labeled A_k. The direct sum of the A_k forms a proper ideal of R. It is easily checked that the left and right annihilators of this ideal are zero, and so R is not right or left Kasch.
The two-by-two upper (or lower) triangular matrix ring is not right or left Kasch.
A ring with right socle zero (i.e. 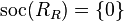$\mathrm{soc}(R_R)=\{0\}$ ) cannot be right Kasch, since the ring contains no minimal right ideals. So, for example, domains which are not division rings are not right or left Kasch.

References

↑ This ideal is necessarily a minimal right ideal.

Faith, Carl (1999), Rings and things and a fine array of twentieth century associative algebra, Mathematical Surveys and Monographs 65, Providence, RI: American Mathematical Society, pp. xxxiv+422, ISBN 0-8218-0993-8, MR 1657671

Kasch, Friedrich (1954), "Grundlagen einer Theorie der Frobeniuserweiterungen", Math. Ann. (in German) 127: 453–474, doi:10.1007/bf01361137, ISSN 0025-5831, MR 0062724

Lam, Tsit-Yuen (1999), Lectures on modules and rings, Graduate Texts in Mathematics No. 189, Berlin, New York: Springer-Verlag, ISBN 978-0-387-98428-5, MR 1653294

Morita, Kiiti (1966), "On S-rings in the sense of F. Kasch", Nagoya Math. J. 27: 687–695, ISSN 0027-7630, MR 0199230

Nicholson, W. K.; Yousif, M. F. (2003), Quasi-Frobenius rings, Cambridge Tracts in Mathematics 158, Cambridge: Cambridge University Press, pp. xviii+307, doi:10.1017/CBO9780511546525, ISBN 0-521-81593-2, MR 2003785

This article is issued from Wikipedia - version of the Sunday, May 11, 2014. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.