Kalman–Yakubovich–Popov lemma
The Kalman–Yakubovich–Popov lemma is a result in system analysis and control theory which states: Given a number  , two n-vectors B, C and an n x n Hurwitz matrix A, if the pair
, two n-vectors B, C and an n x n Hurwitz matrix A, if the pair 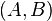 is completely controllable, then a symmetric matrix P and a vector Q satisfying
is completely controllable, then a symmetric matrix P and a vector Q satisfying
exist if and only if
Moreover, the set 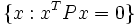 is the unobservable subspace for the pair
is the unobservable subspace for the pair 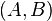 .
.
The lemma can be seen as a generalization of the Lyapunov equation in stability theory. It establishes a relation between a linear matrix inequality involving the state space constructs A, B, C and a condition in the frequency domain.
It was derived in 1962 by Rudolf E. Kalman,[1] who brought together results by Vladimir Andreevich Yakubovich and Vasile Mihai Popov.
Multivariable Kalman–Yakubovich–Popov lemma
Given 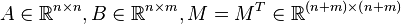 with
with 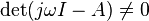 for all
for all 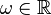 and
and 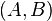 controllable, the following are equivalent:
controllable, the following are equivalent:
- for all
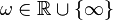
- there exists a matrix
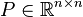 such that
such that 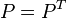 and
and
The corresponding equivalence for strict inequalities holds even if 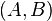 is not controllable. [2]
is not controllable. [2]
References
- ↑ Kalman, Rudolf E. (1963). "Lyapunov functions for the problem of Lur'e in automatic control" (PDF). Proceedings of the National Academy of Sciences 49 (2): 201–205. doi:10.1073/pnas.49.2.201.
- ↑ "Anders Rantzer" (1996). "On the Kalman–Yakubovich–Popov lemma". Systems & Control Letters 28 (1): 7–10. doi:10.1016/0167-6911(95)00063-1.
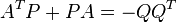
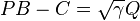
![\gamma+2 Re[C^T (j\omega I-A)^{-1}B]\ge 0](../I/m/2f5c036ca720bcbf6c6cfea845f73c99.png)
![\left[\begin{matrix} (j\omega I - A)^{-1}B \\ I \end{matrix}\right]^* M \left[\begin{matrix} (j\omega I - A)^{-1}B \\ I \end{matrix}\right] \le 0](../I/m/295f121d3b35907b59abe35c477a6afd.png)
![M + \left[\begin{matrix} A^T P + PA & PB \\ B^T P & 0 \end{matrix}\right] \le 0.](../I/m/991c40e6bc55edc80745f176390f6eec.png)