Kallman–Rota inequality

In mathematics, the Kallman–Rota inequality, introduced by Kallman & Rota (1970), is a generalization of the Landau–Kolmogorov inequality to Banach spaces. It states that if A is the infinitesimal generator of a one-parameter contraction semigroup then

\|Af\|^2 \le 4\|f\|\|A^2f\|. \,

References

Kallman, Robert R.; Rota, Gian-Carlo (1970), "On the inequality 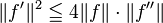$\Vert f^{\prime} \Vert^{2}\leqq4\Vert f\Vert\cdot\Vert f''\Vert$ ", Inequalities, II (Proc. Second Sympos., U.S. Air Force Acad., Colo., 1967), New York: Academic Press, pp. 187–192, MR 0278059 .

This article is issued from Wikipedia - version of the Monday, November 17, 2014. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.