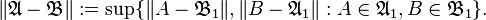Kadison–Kastler metric

In mathematics, the Kadison–Kastler metric is a metric on the space of C^*-algebras on a fixed Hilbert space. It is the Hausdorff distance between the unit balls of the two C^*-algebras, under the norm-induced metric on the space of all bounded operators on that Hilbert space.

It was used by Richard Kadison and Daniel Kastler to study the perturbation theory of von Neumann algebras.

Formal definition

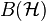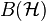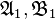Let $\mathcal{H}$ be a Hilbert space and $B(\mathcal{H})$ denote the set of all bounded operators on $\mathcal{H}$ . If $\mathfrak{A}$ and $\mathfrak{B}$ are linear subspaces of $B(\mathcal{H})$ and $\mathfrak{A}_1, \mathfrak{B}_1$ denote their unit balls, respectively, the Kadison–Kastler distance between them is defined as,

\| \mathfrak{A} - \mathfrak{B} \| := \sup \{ \|A - \mathfrak{B}_1\|, \|B - \mathfrak{A}_1 \| : A \in \mathfrak{A}_1, B \in \mathfrak{B}_1 \}.

The above notion of distance defines a metric on the space of C^*-algebras which is called the Kadison-Kastler metric.

References

Kadison, R. V.; Kastler, D., Perturbations of von Neumann algebras I : Stability of Type, American Journal of Mathematics, Vol. XCIV, No. 1 (1972), Pg 38–54.

This article is issued from Wikipedia - version of the Saturday, November 28, 2015. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.