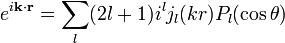Korringa–Kohn–Rostoker approximation
The Korringa–Kohn–Rostoker approximation or KKR method[1][2][3] is used to calculate the electronic band structure of solids. It is a Green's function method which matches the different types of one-electron wave functions and their derivatives which are used in a muffin-tin approximation.
Introduction
In solid state physics the properties of electrons and potentials are determined by the spherical symmetry of the interior of the atoms and the point group symmetry of the crystal lattice. The wave function of an electron and the potential in the KKR method are both composed of two parts. A linear combination of spherical harmonics, which is multiplied by a radial wave function, is used for the wave function on the inside of the atoms where the potential is the potential of the atom. Linear combinations of plane waves are used for the wave function in the regions between the atoms where the potential is constant.
Mathematical formulation
The Schrödinger equation can be expressed like
where 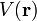 is the potential of the solid and
is the potential of the solid and 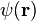 is the wave function of the electron that has to be calculated.
is the wave function of the electron that has to be calculated.
The unperturbed Green's function is defined as the solution of
A plane wave can be expanded as
where 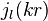 are spherical Bessel functions and
are spherical Bessel functions and 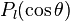 are Legendre polynomials.
are Legendre polynomials.
References
- ↑ J. Korringa (1947). "On the calculation of the energy of a Bloch wave in a metal". Physica XIII (6–7): 392–400. Bibcode:1947Phy....13..392K. doi:10.1016/0031-8914(47)90013-x.
- ↑ W. Kohn, N. Rostoker (1954). "Solution of the Schrödinger Equation in Periodic Lattices with an Application to Metallic Lithium". Phys.Rev. 94 (5): 1111–1120. Bibcode:1954PhRv...94.1111K. doi:10.1103/physrev.94.1111.
- ↑ W. Jones, N. H. March (1973). Theoretical Solid State Physics. Wiley and Sons - Dover Publications. ISBN 0-486-65015-4.
![[\nabla^2 + E]\psi(\bold{r}) = V(\bold{r})\psi(\bold{r})](../I/m/2fd8f22653a74a33a3c2aa7deacf0667.png)
![[\nabla^2 + E]G(\bold{r},\bold{r}') = \delta(\bold{r}-\bold{r}')](../I/m/591ae0a1c66735a828b9ff18fbf04ff8.png)