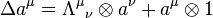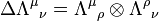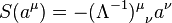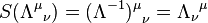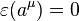K-Poincaré group
In physics and mathematics, the κ-Poincaré group, named after Henri Poincaré, is a quantum group, obtained by deformation of the Poincaré group into an Hopf algebra.
It is generated by the elements 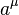 and
and 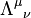 with the usual constraint:
with the usual constraint:
where 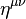 is the Minkowskian metric:
is the Minkowskian metric:
The commutation rules reads:
In the (1 + 1)-dimensional case the commutation rules between 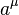 and
and 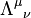 are particularly simple. The Lorentz generator in this case is:
are particularly simple. The Lorentz generator in this case is:
and the commutation rules reads:
The coproducts are classical, and encode the group composition law:
Also the antipodes and the counits are classical, and represent the group inversion law and the map to the identity:
The κ-Poincaré group is the dual Hopf algebra to the K-Poincaré algebra, and can be interpreted as its “finite” version.
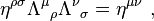
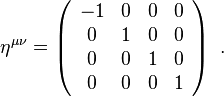
![[a_j ,a_0] = i \lambda a_j ~, \; [a_j,a_k]=0 \,](../I/m/819fff128c181196ff9040129a600df1.png)
![[a^\mu , {\Lambda^\rho}_\sigma ] = i \lambda \left\{ \left( {\Lambda^\rho}_0 - {\delta^\rho}_0 \right) {\Lambda^\mu}_\sigma - \left( {\Lambda^\alpha}_\sigma \eta_{\alpha 0} + \eta_{\sigma 0} \right) \eta^{\rho \mu} \right\} \,](../I/m/7b912b617d970fa52b877dcad38bd74c.png)
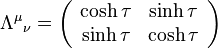
![[ a_0 , \left( \begin{array}{c} \cosh \tau \\ \sinh \tau \end{array} \right) ] = i \lambda ~ \sinh \tau \left( \begin{array}{c} \sinh \tau \\ \cosh \tau \end{array} \right) \,](../I/m/539cd855a8a87e718ca9ff62f410c73c.png)
![[ a_1 , \left( \begin{array}{c} \cosh \tau \\ \sinh \tau \end{array} \right) ] = i \lambda \left( 1- \cosh \tau \right) \left( \begin{array}{c} \sinh \tau \\ \cosh \tau \end{array} \right) \,](../I/m/fc606381b92cdef369c3cd1548419b5c.png)