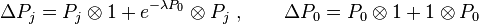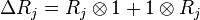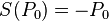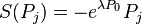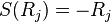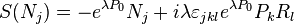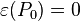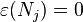K-Poincaré algebra

In physics and mathematics, the κ-Poincaré algebra, named after Henri Poincaré, is a deformation of the Poincaré algebra into an Hopf algebra. In the bicrossproduct basis, introduced by Majid-Ruegg^[1] its commutation rules reads:

$[P_\mu, P_\nu] = 0 \,$

$[R_j , P_0] = 0, \; [R_j , P_k] = i \varepsilon_{jkl} P_l, \; [R_j , N_k] = i \varepsilon_{jkl} N_l, \; [R_j , R_k] = i \varepsilon_{jkl} R_l\,$

$[N_j , P_0] = i P_j, \;[N_j , P_k] = i \delta_{jk} \left( \frac{1 - e^{- 2 \lambda P_0}}{2 \lambda} + \frac{ \lambda }{2} |\vec{P}|^2 \right) - i \lambda P_j P_k, \; [N_j,N_k] = -i \varepsilon_{jkl} R_l\,$

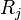Where $P_\mu$ are the translation generators, $R_j$ the rotations and $N_j$ the boosts. The coproducts are:

$\Delta P_j = P_j \otimes 1 + e^{- \lambda P_0} \otimes P_j ~, \qquad \Delta P_0 = P_0 \otimes 1 + 1 \otimes P_0\,$
$\Delta R_j = R_j \otimes 1 + 1 \otimes R_j\,$
$\Delta N_k = N_k \otimes 1 + e^{-\lambda P_0} \otimes N_k + i \lambda \varepsilon_{klm} P_l \otimes R_m .$

The antipodes and the counits:

$S(P_0) = - P_0\,$
$S(P_j) = -e^{\lambda P_0} P_j\,$
$S(R_j) = - R_j\,$
$S(N_j) = -e^{\lambda P_0}N_j +i \lambda \varepsilon_{jkl} e^{\lambda P_0} P_k R_l\,$

$\varepsilon(P_0) = 0\,$
$\varepsilon(P_j) = 0\,$
$\varepsilon(R_j) = 0\,$
$\varepsilon(N_j) = 0\,$

The κ-Poincaré algebra is the dual Hopf algebra to the κ-Poincaré group, and can be interpreted as its “infinitesimal” version.

References

↑ Majid-Ruegg, Phys. Lett. B 334 (1994) 348, ArXiv:hep-th/9405107

This article is issued from Wikipedia - version of the Thursday, August 22, 2013. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.