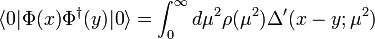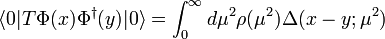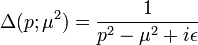Källén–Lehmann spectral representation

Quantum field theory
Feynman diagram
History
Background Field theory Gauge theory Poincaré symmetry Quantum mechanics Spontaneous symmetry breaking
Symmetries Charge conjugation Crossing Parity Time reversal Symmetry in quantum mechanics
Tools Anomaly Effective field theory Expectation value Faddeev–Popov ghosts Feynman diagram Lattice gauge theory LSZ reduction formula Partition function Propagator Quantization Regularization Renormalization Vacuum state Wick's theorem Wightman axioms
Equations Dirac equation Klein–Gordon equation Proca equations Wheeler–DeWitt equation Bargmann–Wigner equations
Standard Model Electroweak interaction Higgs mechanism Quantum chromodynamics Quantum electrodynamics Yang–Mills theory
Incomplete theories Quantum gravity String theory Supersymmetry Technicolor Theory of everything
Scientists C. D. Anderson P. W. Anderson Bethe Bjorken Bogoliubov Brout Callan Coleman DeWitt Dirac Dyson Englert Fermi Feynman Fierz Fock Fröhlich Glashow Gell-Mann Gross Guralnik Heisenberg Higgs Haag Hagen 't Hooft Jordan Kendall Kibble Lamb Landau Lee Majorana Mills Nambu Nishijima Parisi Polyakov Salam Schwinger Skyrme Sudarshan Tomonaga Veltman Ward Weinberg Weisskopf Weyl Wilczek Wilson Yang Yukawa

The Källén–Lehmann spectral representation gives a general expression for the two-point function of an interacting quantum field theory as a sum of free propagators. It was discovered by Gunnar Källén and Harry Lehmann independently.^[1]^[2] This can be written as

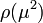\Delta(p)=\int_0^\infty d\mu^2\rho(\mu^2)\frac{1}{p^2-\mu^2+i\epsilon},

where $\rho(\mu^2)$ is the spectral density function that should be positive definite. In a gauge theory, this latter condition cannot be granted but nevertheless a spectral representation can be provided.^[3] This belongs to non-perturbative techniques of quantum field theory.

Mathematical derivation

In order to derive a spectral representation for the propagator of a field 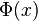$\Phi(x)$ , one consider a complete set of states 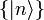$\{|n\rangle\}$ so that, for the two-point function one can write

\langle 0|\Phi(x)\Phi^\dagger(y)|0\rangle=\sum_n\langle 0|\Phi(x)|n\rangle\langle n|\Phi^\dagger(y)|0\rangle.

We can now use Poincaré invariance of the vacuum to write down

\langle 0|\Phi(x)\Phi^\dagger(y)|0\rangle=\sum_n e^{-ip_n\cdot(x-y)}|\langle 0|\Phi(0)|n\rangle|^2.

Let us introduce the spectral density function

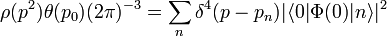\rho(p^2)\theta(p_0)(2\pi)^{-3}=\sum_n\delta^4(p-p_n)|\langle 0|\Phi(0)|n\rangle|^2

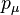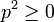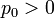We have used the fact that our two-point function, being a function of $p_\mu$ , can only depend on $p^2$ . Besides, all the intermediate states have $p^2\ge 0$ and $p_0>0$ . It is immediate to realize that the spectral density function is real and positive. So, one can write

\langle 0|\Phi(x)\Phi^\dagger(y)|0\rangle = \int\frac{d^4p}{(2\pi)^3}\int_0^\infty d\mu^2e^{-ip\cdot(x-y)}\rho(\mu^2)\theta(p_0)\delta(p^2-\mu^2)

and we freely interchange the integration, this should be done carefully from a mathematical standpoint but here we ignore this, and write this expression as

\langle 0|\Phi(x)\Phi^\dagger(y)|0\rangle = \int_0^\infty d\mu^2\rho(\mu^2)\Delta'(x-y;\mu^2)

being

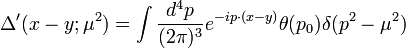\Delta'(x-y;\mu^2)=\int\frac{d^4p}{(2\pi)^3}e^{-ip\cdot(x-y)}\theta(p_0)\delta(p^2-\mu^2)

From CPT theorem we also know that holds an identical expression for 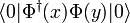$\langle 0|\Phi^\dagger(x)\Phi(y)|0\rangle$ and so we arrive at the expression for the chronologically ordered product of fields

\langle 0|T\Phi(x)\Phi^\dagger(y)|0\rangle = \int_0^\infty d\mu^2\rho(\mu^2)\Delta(x-y;\mu^2)

being now

\Delta(p;\mu^2)=\frac{1}{p^2-\mu^2+i\epsilon}

a free particle propagator. Now, as we have the exact propagator given by the chronologically ordered two-point function, we have obtained the spectral decomposition.

References

↑ Källén, Gunnar (1952). "On the Definition of the Renormalization Constants in Quantum Electrodynamics". Helvetica Physica Acta 25: 417. doi:10.5169/seals-112316(pdf download available)
↑ Lehmann, Harry (1954). "Über Eigenschaften von Ausbreitungsfunktionen und Renormierungskonstanten quantisierter Felder". Nuovo Cimento (in German) (Società Italiana di Fisica) 11 (4): 342–357. doi:10.1007/bf02783624. ISSN 0029-6341.
↑ Strocchi, Franco (1993). Selected Topics on the General Properties of Quantum Field Theory. Singapore: World Scientific. ISBN 981-02-1143-0.

Bibliography

Weinberg, S. (1995). The Quantum Theory of Fields: Volume I Foundations. Cambridge University Press. ISBN 0-521-55001-7.
Peskin, Michael; Schoeder, Daniel (1995). An Introduction to Quantum Field Theory. Perseus Books Group. ISBN 0-201-50397-2.
Zinn-Justin, Jean (1996). Quantum Field Theory and Critical Phenomena (3rd ed.). Clarendon Press. ISBN 0-19-851882-X.

This article is issued from Wikipedia - version of the Thursday, February 11, 2016. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.