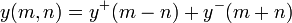Digital waveguide synthesis
Digital waveguide synthesis is the synthesis of audio using a digital waveguide. Digital waveguides are efficient computational models for physical media through which acoustic waves propagate. For this reason, digital waveguides constitute a major part of most modern physical modeling synthesizers.
A lossless digital waveguide realizes the discrete form of d'Alembert's solution of the one-dimensional wave equation as the superposition of a right-going wave and a left-going wave,
where 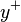 is the right-going wave and
is the right-going wave and 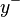 is the left-going wave. It can be seen from this representation that sampling the function
is the left-going wave. It can be seen from this representation that sampling the function 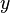 at a given point
at a given point  and time
and time  merely involves summing two delayed copies of its traveling waves. These traveling waves will reflect at boundaries such as the suspension points of vibrating strings or the open or closed ends of tubes. Hence the waves travel along closed loops.
merely involves summing two delayed copies of its traveling waves. These traveling waves will reflect at boundaries such as the suspension points of vibrating strings or the open or closed ends of tubes. Hence the waves travel along closed loops.
Digital waveguide models therefore comprise digital delay lines to represent the geometry of the waveguide which are closed by recursion, digital filters to represent the frequency-dependent losses and mild dispersion in the medium, and often non-linear elements. Losses incurred throughout the medium are generally consolidated so that they can be calculated once at the termination of a delay line, rather than many times throughout.
Waveguides such as acoustic tubes are three-dimensional, but because their lengths are often much greater than their cross-sectional area, it is reasonable and computationally efficient to model them as one-dimensional waveguides. Membranes, as used in drums, may be modeled using two-dimensional waveguide meshes, and reverberation in three-dimensional spaces may be modeled using three-dimensional meshes. Vibraphone bars, bells, singing bowls and other sounding solids (also called idiophones) can be modeled by a related method called banded waveguides where multiple band-limited digital waveguide elements are used to model the strongly dispersive behavior of waves in solids.
The term "digital waveguide synthesis" was coined by Julius O. Smith III who helped develop it and eventually filed the patent. It represents an extension of the Karplus–Strong algorithm. Stanford University owns the patent rights for digital waveguide synthesis and signed an agreement in 1989 to develop the technology with Yamaha.
An extension to DWG synthesis of strings made by Smith is commuted synthesis, wherein the excitation to the digital waveguide contains both string excitation and the body response of the instrument. This is possible because the digital waveguide is linear and makes it unnecessary to model the instrument body's resonances after synthesizing the string output, greatly reducing the number of computations required for a convincing resynthesis.
Prototype software implementations by Smith and colleagues were done in the Synthesis Toolkit (STK).[1][2]
The first musical use of digital waveguide synthesis was in the composition May All Your Children Be Acrobats (1981) by David A. Jaffe, followed by his Silicon Valley Breakdown (1982).
Licensees
- Yamaha
- VL1 (1994) — expensive keyboard (about $10,000 USD)
- VL1m, VL7 (1994) — tone module and less expensive keyboard, respectively
- VP1 (prototype) (1994)
- VL70m (1996) — less expensive tone module
- EX5 (1999) — workstation keyboard that included a VL module
- PLG-100VL, PLG-150VL (1999) — plug-in cards for various Yamaha keyboards, tone modules, and the SWG-1000 high-end PC sound card. The MU100R rack-mount tone module included two PLG slots, pre-filled with a PLG-100VL and a PLG-100VH (Vocal Harmonizer).
- YMF-724, 744, 754, and 764 sound chips for inexpensive DS-XG PC sound cards and motherboards (the VL part only worked on Windows 95, 98, 98SE, and ME, and then only when using .VxD drivers, not .WDM). No longer made, presumably due to conflict with AC-97 and AC-99 sound card standards (which specify 'wavetables' (sample tables) based on Roland’s XG-competing GS sound system, which Sondius-XG [the means of integrating VL instruments and commands into an XG-compliant MIDI stream along with wavetable XG instruments and commands] cannot integrate with). The MIDI portion of such sound chips, when the VL was enabled, was functionally equivalent to an MU50 Level 1 XG tone module (minus certain digital effects) with greater polyphony (up to 64 simultaneous notes, compared to 32 for Level 1 XG) plus a VL70m (the VL adds an additional note of polyphony, or, rather, a VL solo note backed up by the up-to-64 notes of polyphony of the XG wavetable portion). The 724 only supported stereo out, while the others supported various four and more speaker setups. Yamaha’s own card using these was the WaveForce-128, but a number of licensees made very inexpensive YMF-724 sound cards that retailed for as low as $12 at the peak of the technology’s popularity. The MIDI synth portion (both XG and VL) of the YMF chips was actually just hardware assist to a mostly software synth that resided in the device driver (the XG wavetable samples, for instance, were in system RAM with the driver [and could be replaced or added to easily], not in ROM on the sound card). As such, the MIDI synth, especially with VL in active use, took considerably more CPU power than a truly hardware synth would use, but not as much as a pure software synth. Towards the end of their market period, YMF-724 cards could be had for as little as $12 USD brand new, making them by far the least expensive means of obtaining Sondius-XG CL digital waveguide technology. The DS-XG series also included the YMF-740, but it lacked the Sondius-XG VL waveguide synthesis module, yet was otherwise identical to the YMF-744.
- S-YXG100plus-VL Soft Synthesizer for PCs with any sound card (again, the VL part only worked on Windows 95, 98, 98SE, and ME: it emulated a .VxD MIDI device driver). Likewise equivalent to an MU50 (minus certain digital effects) plus VL70m. The non-VL version, S-YXG50, would work on any Windows OS, but had no physical modeling, and was just the MU50 XG wavetable emulator. This was basically the synth portion of the YMF chips implemented entirely in software without the hardware assist provided by the YMF chips. Required a somewhat more powerful CPU than the YMF chips did. Could also be used in conjunction with a YMF-equipped sound card or motherboard to provide up to 128 notes of XG wavetable polyphony and up to two VL instruments simultaneously on sufficiently powerful CPUs.
- S-YXG100plus-PolyVL SoftSynth for then-powerful PCs (e. g. 333+MHz Pentium III), capable of up to eight VL notes at once (all other Yamaha VL implementations except the original VL1 and VL1m were limited to one, and the VL1/1m could do two), in addition to up to 64 notes of XG wavetable from the MU50-emulating portion of the soft synth. Never sold in the USA, but was sold in Japan. Presumably a much more powerful system could be done with today’s multi-GHz dual-core CPUs, but the technology appears to have been abandoned. Hypothetically could also be used with a YMF chipset system to combine their capabilities on sufficiently powerful CPUs.
- Korg
- Technics
- WSA1 (1995) PCM + resonator
- Seer Systems
- Creative WaveSynth (1996) for Creative Labs Sound Blaster AWE64.
- Reality (1997) - one of the earliest professional software synthesizer product by Dave Smith team
- Cakewalk
- Dimension Pro (2005) - software synthesizer for OS X and Windows XP.[4]
References
Further reading
- Daniel Levitin (7 May 1994). "Yamaha VL-1 revolutionizes synthesizer technology". Billboard: 102–103.
- Yamaha VL1. Virtual Acoustic Synthesizer, Sound on Sound, July 1994
- Paul Verna (2 August 1997). "Yamaha, Stanford join forces. Licensing program offers new technologies". Billboard: 56.
- Julius O. Smith (2008). "Digital Waveguide Architectures for Virtual Musical Instruments". In David Havelock, Sonoko Kuwano, Michael Vorländer. Handbook of Signal Processing in Acoustics. Springer. pp. 399–417. ISBN 978-0-387-77698-9.
- Martin Russ (2008). Sound Synthesis and Sampling. Focal Press. pp. 288–289. ISBN 978-0-240-52105-3.
- Brian Heywood (22 Nov 2005) Model behaviour. The technology your PC uses to make sound is usually based on replaying an audio sample. Brian Heywood looks at alternatives., PC Pro
- Stefan Bilbao (2009). Numerical Sound Synthesis: Finite Difference Schemes and Simulation in Musical Acoustics. John Wiley and Sons. pp. 11–14. ISBN 978-0-470-51046-9.
- Lutz Trautmann; Rudolf Rabenstein (2003). Digital sound synthesis by physical modeling using the functional transformation method. Springer. pp. 77–86. ISBN 978-0-306-47875-8.
External links
- Julius O. Smith III's ``A Basic Introduction to Digital Waveguide Synthesis"
- Waveguide Synthesis home page
- Virtual Acoustic Musical Instruments: Review and Update
- Modeling string sounds and wind instruments - Sound on Sound magazine, September 1998
- Jordan Rudess playing on Korg Oasys Youtube recording. Note the use of the joystick to control the vibrato effect of the plucked strings physical model.
- Yamaha VL1 with breath controller vs. traditional synthesizer for wind instruments
| ||||||||||||||