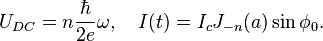Josephson effect

Josephson junction array chip developed by the National Bureau of Standards as a standard volt

The Josephson effect is the phenomenon of supercurrent—i.e. a current that flows indefinitely long without any voltage applied—across a device known as a Josephson junction (JJ), which consists of two superconductors coupled by a weak link. The weak link can consist of a thin insulating barrier (known as a superconductor–insulator–superconductor junction, or S-I-S), a short section of non-superconducting metal (S-N-S), or a physical constriction that weakens the superconductivity at the point of contact (S-s-S).

The Josephson effect is an example of a macroscopic quantum phenomenon. It is named after the British physicist Brian David Josephson, who predicted in 1962 the mathematical relationships for the current and voltage across the weak link.^[1]^[2] The DC Josephson effect had been seen in experiments prior to 1962,^[3] but had been attributed to "super-shorts" or breaches in the insulating barrier leading to the direct conduction of electrons between the superconductors. The first paper to claim the discovery of Josephson's effect, and to make the requisite experimental checks, was that of Philip Anderson and John Rowell.^[4] These authors were awarded patents on the effects that were never enforced, but never challenged.

Before Josephson's prediction, it was only known that normal (i.e. non-superconducting) electrons can flow through an insulating barrier, by means of quantum tunneling. Josephson was the first to predict the tunneling of superconducting Cooper pairs. For this work, Josephson received the Nobel prize in physics in 1973.^[5] Josephson junctions have important applications in quantum-mechanical circuits, such as SQUIDs, superconducting qubits, and RSFQ digital electronics. The NIST standard for one volt is achieved by an array of 19,000 Josephson junctions in series.^[6]

A Dayem bridge is a thin-film variant of the Josephson junction in which the weak link consists of a superconducting wire with dimensions on the scale of a few micrometres or less.^[7]^[8]

The effect

Diagram of a single Josephson junction. A and B represent superconductors, and C the weak link between them.

The basic equations governing the dynamics of the Josephson effect are^[9]

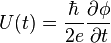U(t) = \frac{\hbar}{2 e} \frac{\partial \phi}{\partial t}

(superconducting phase evolution equation)

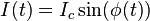\frac{}{} I(t) = I_c \sin (\phi (t))

(Josephson or weak-link current-phase relation)

where U(t) and I(t) are the voltage and current across the Josephson junction, $\phi(t)$ is the "phase difference" across the junction (i.e., the difference in phase factor, or equivalently, argument, between the Ginzburg–Landau complex order parameter of the two superconductors composing the junction), and I_c is a constant, the critical current of the junction. The critical current is an important phenomenological parameter of the device that can be affected by temperature as well as by an applied magnetic field. The physical constant 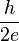$\frac{h}{2 e}$ is the magnetic flux quantum, the inverse of which is the Josephson constant.

Typical I-V characteristic of a superconducting tunnel junction, a common kind of Josephson junction. The scale of the vertical axis is 50 μA and that of the horizontal one is 1 mV. The bar at

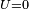\scriptstyle U = 0

represents the DC Josephson effect, while the current at large values of

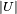\scriptstyle |U|

is due to the finite value of the superconductor bandgap and not reproduced by the above equations.

The three main effects predicted by Josephson follow from these relations:

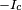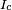The DC Josephson effect: The DC Josephson effect is a direct current crossing the insulator in the absence of any external electromagnetic field, owing to tunneling. This DC Josephson current is proportional to the sine of the phase difference across the insulator, and may take values between $\scriptstyle -I_c$ and $\scriptstyle I_c$ .
The AC Josephson effect: With a fixed voltage 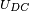$\scriptstyle U_{DC}$ across the junctions, the phase will vary linearly with time and the current will be an AC current with amplitude 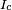$\scriptstyle I_c$ and frequency 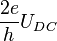$\frac{2e}{h} U_{DC}$ . The complete expression for the current drive 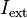$I_\text{ext}$ becomes 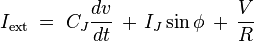$I_\text{ext} \;=\; C_J \frac{dv}{dt} \,+\, I_J \sin \phi \,+\, \frac{V}{R}$ . This means a Josephson junction can act as a perfect voltage-to-frequency converter.
The inverse AC Josephson effect: If the phase takes the form 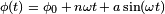$\scriptstyle \phi (t) \;=\; \phi_0 \,+\, n \omega t \,+\, a \sin( \omega t)$ , the voltage and current will be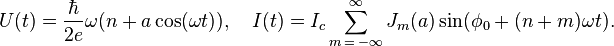; $U(t) = \frac{\hbar}{2 e} \omega ( n + a \cos( \omega t) ), \ \ \ I(t) = I_c \sum_{m \,=\, -\infty}^\infty J_m (a) \sin (\phi_0 + (n + m) \omega t).$

The DC components will then be

U_{DC} = n \frac{\hbar}{2 e} \omega, \ \ \ I(t) = I_c J_{-n} (a) \sin \phi_0.

Hence, for distinct AC voltages, the junction may carry a DC current and the junction acts like a perfect frequency-to-voltage converter.

Applications

The Josephson effect has found wide usage, for example in the following areas:

SQUIDs, or superconducting quantum interference devices, are very sensitive magnetometers that operate via the Josephson effect. They are widely used in science and engineering.
In precision metrology, the Josephson effect provides an exactly reproducible conversion between frequency and voltage. Since the frequency is already defined precisely and practically by the caesium standard, the Josephson effect is used, for most practical purposes, to give the standard representation of a volt, the Josephson voltage standard. However, BIPM has not changed the official SI unit definition.^[10]^[11]
Single-electron transistors are often constructed of superconducting materials, allowing use to be made of the Josephson effect to achieve novel effects. The resulting device is called a "superconducting single-electron transistor."^[12] The Josephson effect is also used for the most precise measurements of elementary charge in terms of the Josephson constant and von Klitzing constant which is related to the quantum Hall effect.
RSFQ digital electronics is based on shunted Josephson junctions. In this case, the junction switching event is associated to the emission of one magnetic flux quantum 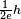$\scriptstyle\frac{1}{2 e}h$ that carries the digital information: the absence of switching is equivalent to 0, while one switching event carries a 1.
Josephson junctions are integral in superconducting quantum computing as qubits such as in a flux qubit or others schemes where the phase and charge act as the conjugate variables.^[13]
Superconducting tunnel junction detectors (STJs) may become a viable replacement for CCDs (charge-coupled devices) for use in astronomy and astrophysics in a few years. These devices are effective across a wide spectrum from ultraviolet to infrared, and also in x-rays. The technology has been tried out on the William Herschel Telescope in the SCAM instrument.
Quiterons and similar superconducting switching devices.
Josephson effect has also been observed in SHeQUIDs, the superfluid helium analog of a dc-SQUID.^[14]

References

↑ Josephson, B. D., "Possible new effects in superconductive tunnelling," Physics Letters 1, 251 (1962) doi:10.1016/0031-9163(62)91369-0
↑ Josephson, B. D. (1974). "The discovery of tunnelling supercurrents". Rev. Mod. Phys. 46 (2): 251–254. Bibcode:1974RvMP...46..251J. doi:10.1103/RevModPhys.46.251.
↑ Josephson, Brian D. (December 12, 1973). "The Discovery of Tunneling Supercurrents (Nobel Lecture)" (PDF).
↑ Anderson, P W; Rowell, J M (1963). "Probable Observation of the Josephson Tunnel Effect". Phys. Rev. Letters 10: 230. Bibcode:1963PhRvL..10..230A. doi:10.1103/PhysRevLett.10.230. |access-date= requires |url= (help)
↑ The Nobel prize in physics 1973, accessed 8-18-11
↑ Steven Strogatz, Sync: The Emerging Science of Spontaneous Order, Hyperion, 2003.
↑ Anderson, P. W., and Dayem, A. H., "Radio-frequency effects in superconducting thin film bridges," Physical Review Letters 13, 195 (1964), doi:10.1103/PhysRevLett.13.195
↑ Dawe, Richard (28 October 1998). "SQUIDs: A Technical Report - Part 3: SQUIDs" (website). http://rich.phekda.org. Retrieved 2011-04-21. External link in |publisher= (help)
↑ Barone, A.; Paterno, G. (1982). Physics and Applications of the Josephson Effect. New York: John Wiley & Sons. ISBN 0-471-01469-9.
↑ International Bureau of Weights and Measures (BIPM), SI brochure, section 2.1.: SI base units, section 2.1.1: Definitions, accessed 22 June 2015
↑ Practical realization of units for electrical quantities (SI brochure, Appendix 2). BIPM, [last updated: 20 February 2007], accessed 22 June 2015.
↑ Fulton, T.A.; et al. (1989). "Observation of Combined Josephson and Charging Effects in Small Tunnel Junction Circuits". Physical Review Letters 63 (12): 1307–1310. Bibcode:1989PhRvL..63.1307F. doi:10.1103/PhysRevLett.63.1307. PMID 10040529.
↑ Bouchiat, V.; Vion, D.; Joyez, P.; Esteve, D.; Devoret, M. H. (1998). "Quantum coherence with a single Cooper pair" (PDF). Physica Scripta T 76: 165. Bibcode:1998PhST...76..165B. doi:10.1238/Physica.Topical.076a00165.
↑ Physics Today, Superfluid helium interferometers, Y. Sato and R. Packard, October 2012, page 31

Authority control	GND: 4222008-7 NDL: 00576613

This article is issued from Wikipedia - version of the Wednesday, December 23, 2015. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.

Josephson effect

The effect

Applications

See also

References