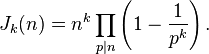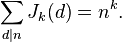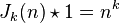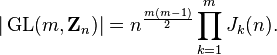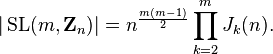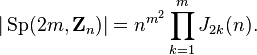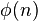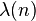Jordan's totient function
Let k be a positive integer. In number theory, Jordan's totient function  of a positive integer n is the number of k-tuples of positive integers all less than or equal to n that form a coprime (k + 1)-tuple together with n. This is a generalisation of Euler's totient function, which is J1. The function is named after Camille Jordan.
of a positive integer n is the number of k-tuples of positive integers all less than or equal to n that form a coprime (k + 1)-tuple together with n. This is a generalisation of Euler's totient function, which is J1. The function is named after Camille Jordan.
Definition
Jordan's totient function is multiplicative and may be evaluated as
Properties
which may be written in the language of Dirichlet convolutions as[1]
and via Möbius inversion as
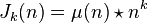 .
.
Since the Dirichlet generating function of μ is 1/ζ(s) and the Dirichlet generating function of nk is ζ(s-k), the series for Jk becomes
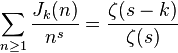 .
.
- An average order of Jk(n) is
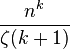 .
.
- The Dedekind psi function is
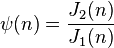 ,
,
and by inspection of the definition (recognizing that each factor in the product
over the primes is a cyclotomic polynomial of p-k), the arithmetic functions
defined by 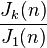 or
or 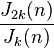 can also be shown to be integer-valued multiplicative functions.
can also be shown to be integer-valued multiplicative functions.
-
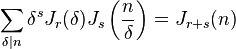 . [2]
. [2]
Order of matrix groups
The general linear group of matrices of order m over Zn has order[3]
The special linear group of matrices of order m over Zn has order
The symplectic group of matrices of order m over Zn has order
The first two formulas were discovered by Jordan.
Examples
Explicit lists in the OEIS are
J2 in ![]() A007434,
J3 in
A007434,
J3 in ![]() A059376,
J4 in
A059376,
J4 in ![]() A059377,
J5 in
A059377,
J5 in ![]() A059378,
J6 up to J10 in
A059378,
J6 up to J10 in ![]() A069091
up to
A069091
up to ![]() A069095.
A069095.
Multiplicative functions defined by ratios are
J2(n)/J1(n) in ![]() A001615,
J3(n)/J1(n) in
A001615,
J3(n)/J1(n) in ![]() A160889,
J4(n)/J1(n) in
A160889,
J4(n)/J1(n) in ![]() A160891,
J5(n)/J1(n) in
A160891,
J5(n)/J1(n) in ![]() A160893,
J6(n)/J1(n) in
A160893,
J6(n)/J1(n) in ![]() A160895,
J7(n)/J1(n) in
A160895,
J7(n)/J1(n) in ![]() A160897,
J8(n)/J1(n) in
A160897,
J8(n)/J1(n) in ![]() A160908,
J9(n)/J1(n) in
A160908,
J9(n)/J1(n) in ![]() A160953,
J10(n)/J1(n) in
A160953,
J10(n)/J1(n) in ![]() A160957,
J11(n)/J1(n) in
A160957,
J11(n)/J1(n) in ![]() A160960.
A160960.
Examples of the ratios J2k(n)/Jk(n) are
J4(n)/J2(n) in ![]() A065958,
J6(n)/J3(n) in
A065958,
J6(n)/J3(n) in ![]() A065959,
and
J8(n)/J4(n) in
A065959,
and
J8(n)/J4(n) in ![]() A065960.
A065960.
Notes
- ↑ Sándor & Crstici (2004) p.106
- ↑ Holden et al in external links The formula is Gegenbauer's
- ↑ All of these formulas are from Andrici and Priticari in #External links
References
- L. E. Dickson (1971) [1919]. History of the Theory of Numbers, Vol. I. Chelsea Publishing. p. 147. ISBN 0-8284-0086-5. JFM 47.0100.04.
- M. Ram Murty (2001). Problems in Analytic Number Theory. Graduate Texts in Mathematics 206. Springer-Verlag. p. 11. ISBN 0-387-95143-1. Zbl 0971.11001.
- Sándor, Jozsef; Crstici, Borislav (2004). Handbook of number theory II. Dordrecht: Kluwer Academic. pp. 32–36. ISBN 1-4020-2546-7. Zbl 1079.11001.
External links
- Andrica, Dorin; Piticari, Mihai (2004). "On some Extensions of Jordan's arithmetical Functions" (PDF). Acta universitatis Apulensis (7). MR 2157944.
- Holden, Matthew; Orrison, Michael; Varble, Michael. "Yet another Generalization of Euler's Totient Function" (PDF).
| ||||||